Título: Introdução à Programação Python Aplicada à Engenharia

Autor: Christian Vladimir Uhdre Mulato

Sumário

1. Apresentação

A presente apostila tem como objetivo introduzir os conceitos fundamentais de programação em linguagem Python com foco na aplicação em problemas práticos de engenharia. Python é uma linguagem moderna, acessível e amplamente adotada nas áreas de ciência, tecnologia e automação de processos industriais. Seu ecossistema rico em bibliotecas permite que engenheiros realizem desde simples análises numéricas até simulações e otimizações complexas com rapidez e precisão. O conteúdo foi organizado em módulos progressivos, partindo dos fundamentos da programação até aplicações reais por meio de projetos. A ideia é desenvolver a lógica de programação, incentivar a experimentação e fortalecer a capacidade de modelar problemas de engenharia utilizando ferramentas computacionais.

Ao final, o leitor será capaz de:

• Compreender os principais conceitos da linguagem Python.
• Resolver problemas matemáticos aplicados à engenharia com auxílio de bibliotecas como NUM_PY, PANDAS, MAT_PLOT_LIB e SCI_PY.
• Modelar, simular e visualizar sistemas físicos e processos.
• Desenvolver soluções computacionais práticas com uma abordagem estruturada.

Esta apostila é indicada para estudantes de cursos técnicos e superiores em engenharia e áreas afins, bem como profissionais que desejam iniciar no uso da programação para aplicações técnicas.

Boa leitura e bons estudos!

• Christian V. Uhdre Mulato
• Engenheiro Químico e Desenvolvedor de Sistemas

Campo Largo – PR

2. Fundamentos da Programação em Python

Este primeiro módulo tem como objetivo estabelecer uma base sólida em programação Python, essencial para todas as aplicações que veremos ao longo desta apostila. Dominar os fundamentos da linguagem é crucial para compreender e desenvolver soluções computacionais eficazes para problemas de engenharia.

Neste módulo, vamos explorar os tipos de dados fundamentais em Python, como números inteiros (INT), números de ponto flutuante (FLOAT), cadeias de caracteres (STR) e valores booleanos (BOOL). Entender como representar e manipular esses diferentes tipos de dados é o primeiro passo para realizar cálculos e processar informações em Python.

Além disso, abordaremos os operadores aritméticos e lógicos, que nos permitem realizar operações matemáticas e tomar decisões lógicas dentro dos nossos programas. A capacidade de realizar cálculos e avaliar condições é fundamental para resolver problemas de engenharia, desde a análise de dados experimentais até a modelagem de sistemas físicos.

Finalmente, introduziremos os conceitos de entrada e saída de dados, ensinando como interagir com o usuário e como ler e escrever informações. Também daremos os primeiros passos na aplicação desses conhecimentos em cálculos simples voltados para a engenharia, preparando o terreno para problemas mais complexos nos módulos seguintes.

Ao concluir estes módulos, você estará apto a escrever programas Python simples, mas poderosos, que podem realizar cálculos, manipular dados e interagir com o mundo exterior, lançando as bases para sua jornada na programação aplicada à engenharia.

2.1. Tipos de Dados em Python

Em Python, assim como em outras linguagens de programação, os dados são classificados em diferentes tipos. Cada tipo de dado possui características e comportamentos específicos, o que permite ao computador interpretar e manipular as informações corretamente.

Nesta seção, vamos explorar os quatro tipos de dados fundamentais: - inteiros (INT), - números de ponto flutuante (FLOAT), - cadeias de caracteres (STR) e - booleanos (BOOL).

2.1.1. Inteiros (INT)

O tipo de dado int representa números inteiros, ou seja, números que não possuem parte decimal. Eles podem ser positivos, negativos ou zero.

Exemplos em engenharia:

• Número de peças em um sistema: numero_pecas = 150
• Quantidade de andares de um edifício: andares = 12
• Número de iterações em um cálculo: iteracoes = 1000

2.1.2. Números de Ponto Flutuante (FLOAT)

O tipo de dado float representa números reais, ou seja, números que podem possuir uma parte decimal.

Exemplos em engenharia:

• Aceleração da gravidade: gravidade = 9.81 (m/s²)
• Tensão em um circuito elétrico: tensao = 220.5 (V)
• Coeficiente de atrito: atrito = 0.25
• Vazão de um fluido: vazao = 2.75 (m³/s)
• Temperatura de um processo: temperatura = 37.5 (°C)

2.1.3. Cadeias de Caracteres (STR)

O tipo de dado str representa texto, ou seja, uma sequência de caracteres. As cadeias de caracteres são delimitadas por aspas simples (’) ou aspas duplas (“).

Exemplos em engenharia:

• Nome de um material: material = "Aço Carbono"
• Descrição de um componente: componente = "Válvula de Segurança"
• Unidade de medida: unidade = "MPa" (MegaPascal)
• Resultado de um ensaio: resultado_ensaio = "Aprovado"

2.1.4. Booleanos (BOOL)

O tipo de dado bool representa valores lógicos, ou seja, verdadeiro (True) ou falso (False). Eles são fundamentais para realizar testes condicionais e controlar o fluxo de execução de um programa.

Exemplos em engenharia:

• Status de um sensor: sensor_ligado = True
• Verificação de um limite: temperatura_acima_limite = False
• Condição de falha: falha_detectada = False
• Estado de uma válvula: valvula_aberta = True

Compreender esses tipos de dados é essencial para escrever programas que manipulem informações de forma correta e eficiente em aplicações de engenharia.

2.1.5. Exemplo: Cálculo da Tensão em um Resistor

Imagine que você precisa calcular a tensão em um resistor usando a Lei de Ohm (V = I * R), onde: - V é a tensão (em Volts) - I é a corrente (em Amperes) - R é a resistência (em Ohms)

Além disso, vamos verificar se a potência dissipada no resistor (P = V * I) excede um valor limite.

Código em Python:

# Definição das variáveis

# Corrente elétrica (float)
corrente = 2.0  # Amperes

# Resistência elétrica (float)
resistencia = 10.0  # Ohms

# Limite de potência (float)
potencia_limite = 20.0  # Watts

# Nome do resistor (string)
nome_resistor = "R1"

# Cálculo da tensão (float)
tensao = corrente * resistencia

# Cálculo da potência (float)
potencia = tensao * corrente

# Verificação da potência (bool)
potencia_excede_limite = potencia > potencia_limite

# Exibição dos resultados
print("Cálculo da Tensão e Potência em um Resistor")
print("------------------------------------------")
print("Nome do Resistor:", nome_resistor)
print("Corrente (A):", corrente)
print("Resistência (Ω):", resistencia)
print("Tensão (V):", tensao)
print("Potência (W):", potencia)
print("Potência excede o limite?", potencia_excede_limite)

# Conversão de tipo (demonstração)
# Converter a tensão para inteiro (truncando a parte decimal)
tensao_inteira = int(tensao)
print("Tensão (V, inteiro):", tensao_inteira)

Como usar este código no Visual Studio Code:

1. Abra o Visual Studio Code.
2. Crie um arquivo e salve-o como 01_codigo_calculo_resistor.py.
3. Copie e cole o código acima no arquivo.
4. Execute o código:
   • Clique com o botão direito no editor e selecione “Executar Python no Terminal”.
   • Ou abra o terminal integrado e digite:
     python 01_codigo_calculo_resistor.py
5. Observe a saída no terminal.

Explicação do Código:

• Tipos de Dados:
  O código demonstra o uso de float para grandezas físicas, str para o nome do resistor e bool para o resultado da comparação.
• Cálculos:
  Realiza cálculos típicos de engenharia elétrica usando operadores aritméticos.
• Tomada de Decisão:
  Utiliza uma expressão booleana para simular uma verificação de segurança.
• Saída Formatada:
  Imprime os resultados de forma clara.
• Conversão de Tipo:
  Demonstra como converter um valor float para int.

Resultado:

Cálculo da Tensão e Potência em um Resistor
------------------------------------------
Nome do Resistor: R1
Corrente (A): 2.0
Resistência (Ω): 10.0
Tensão (V): 20.0
Potência (W): 40.0
Potência excede o limite? True
Tensão (V, inteiro): 20

Este exemplo prático mostra como os tipos de dados fundamentais são aplicados em um problema simples de engenharia, combinando cálculo, lógica e representação de informações do mundo real.

2.1.6. Exemplo: Simulação da Trajetória de um Projétil

Neste exemplo, vamos simular a trajetória de um projétil lançado sob um ângulo e com uma velocidade inicial, e gerar um gráfico da trajetória. Este exemplo combina física básica com a visualização de dados.

Código em Python:

import matplotlib.pyplot as plt
import math

# Dados de entrada (tipos float e int)
velocidade_inicial = 20.0  # m/s
angulo_graus = 45       # graus
angulo_radianos = math.radians(angulo_graus) # conversão para radianos
gravidade = 9.81       # m/s²
tempo_total = (2 * velocidade_inicial * math.sin(angulo_radianos)) / gravidade

# Listas para armazenar os pontos da trajetória (listas de floats)
tempos = []
posicoes_x = []
posicoes_y = []

# Cálculo da trajetória
intervalo_tempo = 0.1  # segundos
tempo = 0.0

while tempo <= tempo_total:
    tempos.append(tempo)
    posicao_x = velocidade_inicial * math.cos(angulo_radianos) * tempo
    posicao_y = velocidade_inicial * math.sin(angulo_radianos) * tempo - 0.5 * gravidade * tempo**2
    posicoes_x.append(posicao_x)
    posicoes_y.append(posicao_y)
    tempo += intervalo_tempo

# Nome do projétil (string)
nome_projétil = "Projétil A"

# Geração do gráfico
plt.plot(posicoes_x, posicoes_y)
plt.title("Trajetória de um Projétil")
plt.xlabel("Distância Horizontal (m)")
plt.ylabel("Altura (m)")
plt.grid(True)

# Adicionando informações textuais ao gráfico
plt.text(0, max(posicoes_y) * 0.9, f"Velocidade Inicial: {velocidade_inicial} m/s", fontsize=9)
plt.text(0, max(posicoes_y) * 8, f"Ângulo: {angulo_graus} graus", fontsize=9)
plt.text(0, max(posicoes_y) * 0.7, nome_projétil, fontsize=12, color='red')

plt.show()

# Imprimindo informações relevantes (demonstração de uso de tipos)
print(f"Tempo total de voo: {tempo_total:.2f} s")  # Formatação de float
print(f"Tipo da variável 'nome_projétil': {type(nome_projétil)}") # Mostrando o tipo
print(f"A altura máxima atingida foi: {max(posicoes_y):.2f} m")

Resultado:

Tempo total de voo: 2.04 s
Tipo da variável 'nome_projétil': <class 'str'>
A altura máxima atingida foi: 10.20 m

Como usar este código no Visual Studio Code: 1. Abra o Visual Studio Code. 2. Crie um arquivo e salve-o como 02_codigo_trajetoria_projetil.py. 3. Copie e cole o código acima no arquivo. 4. Certifique-se de ter o Matplotlib instalado. Se não tiver, abra o terminal no VS Code e digite: pip install matplotlib e pressione Enter. 5. Execute o código da mesma forma que no exemplo anterior. 6. Observe a saída: Além da saída no terminal, uma janela com o gráfico da trajetória do projétil será exibida.

Explicação do Código:

Tipos de Dados: - FLOAT: Usado para velocidade, ângulo (em radianos), gravidade, tempo e as posições x e y. - INT: Usado para o ângulo em graus. - STR: Usado para o nome do projétil. - LIST: Usado para armazenar sequências de valores de tempo, posições x e posições y. Listas são estruturas de dados que armazenam múltiplos valores do mesmo tipo (neste caso, float).

Cálculos: O código realiza cálculos de física para determinar a trajetória do projétil, decompondo a velocidade inicial em componentes horizontal e vertical e usando as equações do movimento uniformemente variado.

Visualização: A biblioteca matplotlib.pyplot é usada para criar o gráfico da trajetória. plt.plot() desenha a linha, plt.title(), plt.xlabel(), plt.ylabel() e plt.grid() definem o título, rótulos dos eixos e a grade do gráfico, respectivamente. plt.show() exibe o gráfico. plt.text() adiciona texto informativo ao gráfico.

Estruturas de Dados: As listas tempos, posicoes_x e posicoes_y são usadas para armazenar múltiplos valores de dados, o que é essencial para plotar o gráfico.

Conversão de Tipo: A função math.radians() converte o ângulo de graus para radianos, demonstrando a conversão entre tipos relacionados.

Formatação de Saída: O uso de f-strings (strings formatadas) com especificadores de formatação (:.2f) permite controlar o número de casas decimais na saída. type() é usado para exibir o tipo de uma variável.

Este exemplo é mais complexo e demonstra como os tipos de dados são usados em conjunto com cálculos matemáticos e bibliotecas de visualização para resolver e apresentar um problema de engenharia de forma completa.

Resultado:

2.2. Operadores Aritméticos e Lógicos em Python

Em Python, operadores são símbolos especiais que realizam operações em valores (chamados de operandos). Eles são essenciais para realizar cálculos, comparações e manipular dados em geral. Nesta seção, vamos explorar os operadores aritméticos e lógicos, que são fundamentais para a programação em engenharia.

2.2.1. Operadores Aritméticos

Código Python:

# Exemplo de uso de operadores aritméticos
a = 10
b = 5

soma = a + b
subtracao = a - b
multiplicacao = a * b
divisao = a / b

print("Soma:", soma)
print("Subtração:", subtracao)
print("Multiplicação:", multiplicacao)
print("Divisão:", divisao)

Resultado:

Soma: 15
Subtração: 5
Multiplicação: 50
Divisão: 2.0

Os operadores aritméticos são usados para realizar operações matemáticas básicas.

Adição (+): Soma dois valores. Exemplo: forca1 + forca2 (soma de duas forças)

Subtração (-): Subtrai o segundo valor do primeiro. Exemplo: temperatura_final - temperatura_inicial (variação de temperatura)

**Multiplicação (*):** Multiplica dois valores. Exemplo: comprimento * largura (área de uma superfície)

Divisão (/): Divide o primeiro valor pelo segundo (sempre retorna um FLOAT). Exemplo: distancia / tempo (velocidade média)

Divisão Inteira (//): Divide o primeiro valor pelo segundo e retorna a parte inteira do resultado (truncando a parte decimal). Exemplo: total_pecas // pecas_por_caixa (número de caixas completas)

Módulo (%): Retorna o resto da divisão do primeiro valor pelo segundo. Exemplo: total_segundos % 60 (obter os segundos restantes após dividir por 60)

Exponenciação ():** Eleva o primeiro valor à potência do segundo valor. Exemplo: base ** altura

2.2.2. Operadores Lógicos

Os operadores lógicos são usados para combinar ou negar expressões lógicas (valores booleanos True ou False).

AND (and): Retorna True se ambas as expressões forem True. Exemplo: temperatura > temperatura_minima and pressao < pressao_maxima (verificar se a temperatura está dentro da faixa e a pressão também)

OR (or): Retorna True se pelo menos uma das expressões for True. Exemplo: nivel_tanque < nivel_minimo or valvula_emergencia_aberta (verificar se o nível do tanque está baixo ou a válvula de emergência está aberta)

NOT (not): Nega uma expressão (inverte seu valor lógico). Exemplo: not sensor_ativado (verificar se o sensor não está ativado)

2.2.3. Exemplos Aplicados à Engenharia

1) Cálculo da Área de um Retângulo:

comprimento = 10.5  # metros (float)
largura = 5.0     # metros (float)
area = comprimento * largura  # metros quadrados (float)
print("Área do retângulo:", area, "m²")

Resultado:

Área do retângulo: 52.5 m²

2) Verificação de Condições de Segurança:

pressao = 250.0  # PSI (float)
temperatura = 120.0 # graus Celsius (float)
pressao_maxima = 240.0 # PSI (float)
temperatura_maxima = 110.0 # graus Celsius (float)

seguro = pressao <= pressao_maxima and temperatura <= temperatura_maxima # bool

print("Condições de operação seguras:", seguro)

Resultado:

Condições de operação seguras: False

3) Cálculo de Força Resultante:

massa = 5.0  # kg (float)
aceleracao = 9.8  # m/s² (float)
forca_resultante = massa * aceleracao  # N (float)
print("Força resultante:", forca_resultante, "N")

Resultado:

Força resultante: 49.0 N

Este texto fornece uma base sólida sobre operadores aritméticos e lógicos, juntamente com exemplos práticos de como eles são usados em contextos de engenharia.

2.2.4. Exercício Proposto: Cálculo de Área e Perímetro de um Terreno e Verificação de Viabilidade

Descrição:

Um engenheiro civil precisa desenvolver um programa em Python para auxiliar no cálculo da área e perímetro de um terreno retangular e verificar se ele atende a certos critérios de viabilidade para construção.

Requisitos:

1. Entrada de Dados:
   • O programa deve solicitar ao usuário que insira o comprimento e a largura do terreno em metros.
   • O programa deve solicitar ao usuário a área mínima permitida para construção no local.
2. Cálculos:
   • Calcular a área do terreno (área = comprimento * largura).
   • Calcular o perímetro do terreno (perímetro = 2 * (comprimento + largura)).
3. Verificação de Viabilidade:
   • Verificar se a área do terreno é maior ou igual à área mínima permitida para construção.
   • Verificar se o perímetro do terreno é menor que um valor máximo (por exemplo, 100 metros - este valor pode ser fixo no programa).
4. Saída de Dados:
   • Exibir a área e o perímetro do terreno com duas casas decimais.
   • Exibir uma mensagem indicando se o terreno é viável para construção, com base nos critérios de área e perímetro.

Exemplo de Interação:

Digite o comprimento do terreno (m): 50
Digite a largura do terreno (m): 30
Digite a área mínima permitida para construção (m²): 1000
Área do terreno: 1500.00 m²
Perímetro do terreno: 160.00 m
Terreno viável para construção: Sim

Dicas: - Use os tipos de dados float para representar as medidas do terreno e a área mínima. - Use os operadores aritméticos *, + e / para realizar os cálculos. - Use os operadores lógicos >= e < e o operador and para realizar as verificações de viabilidade. - Use a função input() para obter os dados do usuário. - Use a função print() para exibir os resultados. - Use f-strings para formatar a saída com duas casas decimais.

Código Python de Exemplo:

# Solicitar entrada do usuário
comprimento = float(input("Digite o comprimento do terreno (m): "))
largura = float(input("Digite a largura do terreno (m): "))
area_minima = float(input("Digite a área mínima permitida para construção (m²): "))

# Calcular área e perímetro
area = comprimento * largura
perimetro = 2 * (comprimento + largura)

# Verificar viabilidade
viavel = area >= area_minima and perimetro < 100

# Exibir resultados
print(f"Área do terreno: {area:.2f} m²")
print(f"Perímetro do terreno: {perimetro:.2f} m")
print(f"Terreno viável para construção: {'Sim' if viavel else 'Não'}")

Resultado:

Área do terreno: 1500.00 m²
Perímetro do terreno: 160.00 m
Terreno viável para construção: Sim

Este exercício combina o uso de tipos de dados, operadores aritméticos e lógicos em um contexto prático de engenharia civil, proporcionando uma aplicação mais completa dos conceitos aprendidos.

2.2.5. Exercício Proposto: Análise da Deformação de uma Viga

Descrição:

Um engenheiro mecânico precisa analisar a deformação de uma viga sob diferentes cargas. O programa em Python deve calcular a deflexão da viga em função da posição ao longo do seu comprimento e gerar um gráfico da deflexão.

Requisitos:

1. Entrada de Dados:
   • O programa deve solicitar ao usuário que insira o comprimento da viga (L) em metros.
   • O programa deve solicitar ao usuário o módulo de elasticidade do material da viga (E) em Pascal (Pa).
   • O programa deve solicitar ao usuário o momento de inércia da seção transversal da viga (I) em m⁴.
   • O programa deve solicitar ao usuário o tipo de carregamento (1 para carga uniforme, 2 para carga pontual no meio).
   • Se o carregamento for uniforme, solicitar a intensidade da carga (w) em N/m.
   • Se o carregamento for pontual, solicitar a magnitude da carga (P) em N.
2. Cálculos:

   • Calcular a deflexão (y) da viga em função da posição (x) ao longo do comprimento, usando as seguintes fórmulas:

   • Deflexão para Carga Uniforme: y = (w / (24 * E * I)) * (-x⁴ + 2 * L * x³ - L³ * x)

   • Deflexão para Carga Pontual: ``` Para 0 ≤ x ≤ L/2: y = (P * x / (48 * E * I)) * (3 * L² - 4 * x²)

     Para L/2 < x ≤ L: y = (P * (L - x) / (48 * E * I)) * (3 * L² - 4 * (L - x)²) ```

   Onde:
   • y = Deflexão da viga
   • x = Posição ao longo do comprimento da viga
   • w = Intensidade da carga uniforme
   • P = Magnitude da carga pontual
   • L = Comprimento da viga
   • E = Módulo de elasticidade
   • I = Momento de inércia
3. Geração do Gráfico:
   • Usar a biblioteca matplotlib para gerar um gráfico da deflexão (y) em função da posição (x).
   • O gráfico deve ter título, rótulos nos eixos e grade.
4. Saída de Dados:
   • Exibir os valores de entrada (L, E, I, w ou P).
   • Exibir o valor máximo da deflexão.
   • Salvar o gráfico em um arquivo PNG.

Exemplo de Interação:

Digite o comprimento da viga (m): 5
Digite o módulo de elasticidade (Pa): 200000000000
Digite o momento de inércia (m^4): 0.0001
Digite o tipo de carregamento (1-Uniforme, 2-Pontual): 1
Digite a intensidade da carga (N/m): 1000

Código Python de Exemplo:

import matplotlib.pyplot as plt

# Entrada de dados
L = float(input("Digite o comprimento da viga (m): "))
E = float(input("Digite o módulo de elasticidade (Pa): "))
I = float(input("Digite o momento de inércia (m^4): "))
tipo_carregamento = int(input("Digite o tipo de carregamento (1-Uniforme, 2-Pontual): "))

if tipo_carregamento == 1:
    w = float(input("Digite a intensidade da carga uniforme (N/m): "))
    P = 0
elif tipo_carregamento == 2:
    P = float(input("Digite a magnitude da carga pontual (N): "))
    w = 0
else:
    print("Tipo de carregamento inválido.")
    exit()

# Cálculo da deflexão
num_pontos = 100
x_valores = [i * L / num_pontos for i in range(num_pontos + 1)]
y_valores = []

for x in x_valores:
    if tipo_carregamento == 1:
        y = (w / (24 * E * I)) * (-x**4 + 2 * L * x**3 - L**3 * x)
    elif tipo_carregamento == 2:
        if 0 <= x <= L / 2:
            y = (P * x / (48 * E * I)) * (3 * L**2 - 4 * x**2)
        else:
            y = (P * (L - x) / (48 * E * I)) * (3 * L**2 - 4 * (L - x)**2)
    y_valores.append(y)

# Geração do gráfico
plt.plot(x_valores, y_valores)
plt.title("Deflexão da Viga")
plt.xlabel("Posição (m)")
plt.ylabel("Deflexão (m)")
plt.grid(True)
plt.savefig("deflexao_viga.png")
plt.show()

# Saída de dados
print("\nComprimento da viga:", L, "m")
print("Módulo de elasticidade:", E, "Pa")
print("Momento de inércia:", I, "m^4")
if tipo_carregamento == 1:
    print("Carga uniforme:", w, "N/m")
elif tipo_carregamento == 2:
    print("Carga pontual:", P, "N")
print("Deflexão máxima:", max(y_valores), "m")
print("Gráfico da deflexão salvo como deflexao_viga.png")

Resultado:

Digite o comprimento da viga (m): 5
Digite o módulo de elasticidade (Pa): 200000000000
Digite o momento de inércia (m^4): 0.0001
Digite o tipo de carregamento (1-Uniforme, 2-Pontual): 1
Digite a intensidade da carga (N/m): 1000
Deflexão máxima: 0.01042 m
Gráfico da deflexão salvo como deflexao_viga.png

Gráfico:

Este exercício é mais completo e envolve: - Entrada de dados variados (comprimento, propriedades do material, tipo e intensidade de carregamento). - Cálculos condicionais (usando IF e ELIF) para aplicar a fórmula correta de deflexão. - Uso de listas para armazenar múltiplos valores de X e Y para plotagem. - Geração de um gráfico com matplotlib para visualizar a deformação da viga. - Saída formatada dos resultados.

Este tipo de problema é representativo de análises comuns em engenharia mecânica e demonstra a utilidade da programação para resolver problemas complexos e visualizar resultados.

2.2.6. Curiosidade – Mecânica dos Sólidos

No exemplo do cálculo da deflexão da viga, a teoria física aplicada é a da Mecânica dos Sólidos, especificamente a Teoria da Elasticidade Linear para vigas. As fórmulas utilizadas derivam das equações da linha elástica, que descrevem o comportamento de vigas sob flexão.

Fórmulas e Teoria Detalhada:

1. Deflexão para Carga Uniforme:

Fórmula:

y = (w / (24 * E * I)) * (-x⁴ + 2 * L * x³ - L³ * x)

Teoria: - Esta fórmula é derivada da equação diferencial da linha elástica para uma viga submetida a uma carga uniformemente distribuída. - A equação da linha elástica relaciona a curvatura da viga com o momento fletor interno. - As suposições incluem que o material da viga é linearmente elástico, homogêneo e isotrópico, e que as deflexões são pequenas em comparação com o comprimento da viga.

2. Deflexão para Carga Pontual:

Fórmula:

    Para 0 <= x <= L/2:
    y = (P * x / (48 * E * I)) * (3 * L² - 4 * x²)

    Para L/2 < x <= L:
    y = (P * (L - x) / (48 * E * I)) * (3 * L² - 4 * (L - x)²)

Teoria: - Estas fórmulas são derivadas da equação da linha elástica para uma viga com uma carga concentrada aplicada no meio do vão. - Existem duas equações porque o comportamento da viga é diferente à esquerda e à direita da carga pontual. - As mesmas suposições da teoria da carga uniforme se aplicam aqui.

Onde: - y = Deflexão da viga (deslocamento vertical) - x = Posição ao longo do comprimento da viga - L = Comprimento total da viga - E = Módulo de elasticidade do material (resistência do material à deformação elástica) - I = Momento de inércia da seção transversal da viga (resistência da seção da viga à flexão) - w = Intensidade da carga uniforme (força por unidade de comprimento) - P = Magnitude da carga pontual (força concentrada)

Importância na Engenharia:

Essas fórmulas e a teoria da flexão de vigas são fundamentais na engenharia estrutural e mecânica. Engenheiros usam esses princípios para: - Dimensionar vigas: Determinar as dimensões e o material de uma viga para suportar cargas com segurança e dentro de limites aceitáveis de deflexão. - Analisar estruturas: Calcular as tensões e deformações em estruturas que contêm vigas. - Projetar máquinas: Garantir que os componentes de máquinas que atuam como vigas (eixos, suportes etc.) funcionem corretamente.

Compreender a teoria por trás das fórmulas é crucial para aplicar corretamente os resultados dos cálculos e garantir a segurança e a eficiência dos projetos de engenharia.

2.3. Entrada e Saída de Dados em Python

Em programação, a entrada e saída de dados referem-se à forma como um programa recebe informações (entrada) e como ele apresenta os resultados (saída). Em Python, as funções input() e print() são as mais comuns para realizar essas operações.

2.3.1. Entrada de Dados: input()

A função input() permite que o programa receba dados do usuário através do teclado.

• Sintaxe: variavel = input("Mensagem para o usuário")

• Funcionamento:

  1. A função input() exibe a mensagem para o usuário (prompt) na tela.
  2. O usuário digita a informação e pressiona Enter.
  3. A função input() retorna a informação digitada como uma string.
  4. A informação retornada é atribuída à variável.

• Importante: Mesmo que o usuário digite números, a função input() sempre retorna uma STRING. Se você precisar usar a entrada como número, será necessário convertê-la explicitamente usando as funções int() (para inteiros) ou float() (para números de ponto flutuante).

• Exemplos em engenharia:

Solicitar ao usuário o diâmetro de um tubo:

diametro_tubo = float(input("Digite o diâmetro do tubo (em metros): "))
print("Diâmetro do tubo:", diametro_tubo, "m")

Pedir a vazão de um fluido:

vazao_fluido = float(input("Digite a vazão do fluido (em m³/s): "))
print("Vazão do fluido:", vazao_fluido, "m³/s")

Obter o nome de um material:

nome_material = input("Digite o nome do material: ")
print("Nome do material:", nome_material)

2.3.2. Saída de Dados: print()

A função print() exibe informações na tela do computador.

• Sintaxe: print(argumento1, argumento2, ..., argumentoN)
• Funcionamento:
  1. A função print() exibe os valores dos argumentos na tela.
  2. Os argumentos podem ser variáveis, valores literais (números, strings etc.) ou expressões.
  3. Múltiplos argumentos são separados por vírgula, e a função print() os exibe separados por espaço.
  4. Por padrão, a função print() adiciona uma quebra de linha ao final da saída, ou seja, o próximo print() exibirá na linha seguinte.
• Formatação de saída: Python oferece várias maneiras de formatar a saída para torná-la mais clara e organizada. As f-strings (strings formatadas) são uma forma conveniente de formatar strings incluindo variáveis.
• Exemplos em engenharia:

Exibir o resultado de um cálculo:

resultado = 2 + 2
print("O resultado da soma é:", resultado)

Mostrar uma mensagem de alerta:

print("Atenção: Verifique os dados de entrada!")

Exibir informações formatadas:

nome_material = "Aço"
diametro_tubo = 0.1
print(f"Dados do tubo:")
print(f"Nome do material: {nome_material}")
print(f"Diâmetro: {diametro_tubo} m")

Apresentar os dados de um experimento:

temperatura = 25.5
pressao = 101.3
print(f"Dados do experimento:")
print(f"Temperatura: {temperatura} °C")
print(f"Pressão: {pressao} kPa")

A habilidade de obter dados do usuário e apresentar resultados de forma clara é fundamental para criar programas interativos e úteis em engenharia.

2.3.3. Exercício Proposto: Cálculo de Conversão em um Reator

Descrição:

Um engenheiro químico precisa de um programa para calcular a conversão de um reagente em um reator.
O programa deve solicitar ao usuário a quantidade inicial do reagente, a quantidade final após a reação e exibir a conversão calculada. Além disso, deve pedir informações sobre o tipo de reator e o tempo de reação.

Requisitos:

1. Entrada de Dados:
   • O programa deve solicitar ao usuário o nome do reagente (str).
   • O programa deve solicitar ao usuário a quantidade inicial do reagente em mols (float).
   • O programa deve solicitar ao usuário a quantidade final do reagente em mols (float).
   • O programa deve solicitar ao usuário o tipo do reator (str).
   • O programa deve solicitar ao usuário o tempo de reação em minutos (float).
2. Cálculo:

Calcular a conversão do reagente usando a fórmula:

conversao = (quantidade_inicial - quantidade_final) / quantidade_inicial * 100

3. Saída de Dados:
   • Exibir o nome do reagente.
   • Exibir a quantidade inicial e final do reagente, formatadas com 2 casas decimais.
   • Exibir a conversão calculada, formatada como porcentagem com 2 casas decimais (ex: 80.00%).
   • Exibir o tipo do reator e o tempo de reação.

Exemplo de Interação:

Digite o nome do reagente: Amoníaco
Digite a quantidade inicial do reagente (em mols): 10.0
Digite a quantidade final do reagente (em mols): 2.0
Digite o tipo do reator: Reator de Batelada
Digite o tempo de reação (em minutos): 30.0
Reagente: Amoníaco
Quantidade inicial: 10.00 mols
Quantidade final: 2.00 mols
Conversão: 80.00%
Tipo do reator: Reator de Batelada
Tempo de reação: 30.00 minutos

Código Python de Exemplo:

# Solicitar entrada do usuário
nome_reagente = input("Digite o nome do reagente: ")
quantidade_inicial = float(input("Digite a quantidade inicial do reagente (em mols): "))
quantidade_final = float(input("Digite a quantidade final do reagente (em mols): "))
tipo_reator = input("Digite o tipo do reator: ")
tempo_reacao = float(input("Digite o tempo de reação (em minutos): "))

# Cálculo da conversão
conversao = (quantidade_inicial - quantidade_final) / quantidade_inicial * 100

# Exibir resultados
print(f"\nReagente: {nome_reagente}")
print(f"Quantidade inicial: {quantidade_inicial:.2f} mols")
print(f"Quantidade final: {quantidade_final:.2f} mols")
print(f"Conversão: {conversao:.2f}%")
print(f"Tipo do reator: {tipo_reator}")
print(f"Tempo de reação: {tempo_reacao:.2f} minutos")

Dicas: - Use a função input() para obter os dados do usuário. - Use os tipos de dados float e str para armazenar os valores. - Lembre-se de converter as entradas numéricas de input() para float. - Use f-strings para formatar a saída, especialmente a conversão (:.2f%).

Figura 2.3.1 – Esquema Técnico

+---------------------+
|   Programa Python   |
+---------------------+
         ||
+---------------------+
|   Entrada de Dados  |
+---------------------+
         ||
+---------------------+
|       input()       |
+---------------------+
         ||
+-----------------------------+
|  Dados do Usuário (Teclado) |
+-----------------------------+
         ||
+-------------------------------+
| Processamento (Cálculos, Lógica) |
+-------------------------------+
         ||
+---------------------+
|   Saída de Dados    |
+---------------------+
         ||
+---------------------+
|      print()        |
+---------------------+
         ||
+---------------------+
|    Resultados       |
|      (Tela)         |
+---------------------+
         ||

Descrição do Esquema: 1. Programa Python: Representa o código Python que o engenheiro escreve para resolver um problema específico (e.g., cálculo de tensões, simulação de um circuito). 2. input() function: Indica o ponto onde o programa interage com o usuário para receber dados. A função input() aguarda que o usuário digite informações através do teclado. 3. Dados do Usuário (Teclado): Mostra a entrada de dados feita pelo usuário, que podem ser valores numéricos, texto etc. 4. Processamento (Cálculos, Lógica): Representa a parte do programa onde os dados de entrada são manipulados, cálculos são realizados, decisões lógicas são tomadas etc. 5. print() function: Indica o ponto onde o programa exibe os resultados ou informações para o usuário. A função print() envia a saída para a tela. 6. Resultados (Tela): Mostra a saída do programa, que pode incluir números, texto, mensagens, gráficos (em módulos mais avançados) etc.

Detalhes Técnicos: - O esquema é genérico e se aplica a muitos programas que interagem com o usuário. - As setas indicam a direção do fluxo de dados. - Os retângulos representam componentes ou processos do programa. - Não há cores para manter o estilo técnico.

Este esquema ajuda a visualizar o fluxo de informações em um programa Python, desde a obtenção dos dados até a apresentação dos resultados.

Código Python:

# Entrada de dados
nome_reagente = input("Digite o nome do reagente: ")
quantidade_inicial = float(input("Digite a quantidade inicial de " + nome_reagente + " (mols): "))
quantidade_final = float(input("Digite a quantidade final de " + nome_reagente + " (mols): "))
tipo_reator = input("Digite o tipo do reator: ")
tempo_reacao = float(input("Digite o tempo de reação (minutos): "))

# Cálculo da conversão
conversao = (quantidade_inicial - quantidade_final) / quantidade_inicial

# Saída de dados
print("\nReagente:", nome_reagente)
print(f"Quantidade Inicial: {quantidade_inicial:.2f} mols")
print(f"Quantidade Final: {quantidade_final:.2f} mols")
print(f"Conversão: {conversao * 100:.2f} %")
print("Tipo do Reator:", tipo_reator)
print("Tempo de Reação:", tempo_reacao, "minutos")

Resultado:

Reagente: Amoníaco
Quantidade Inicial: 10.00 mols
Quantidade Final: 2.00 mols
Conversão: 80.00 %
Tipo do Reator: Reator de Batelada
Tempo de Reação: 30.00 minutos

Este exercício aborda um problema prático de engenharia química e reforça o uso de entrada e saída de dados com formatação.

2.4. Primeiros Cálculos Aplicados à Engenharia

Nesta seção, vamos explorar como aplicar os fundamentos da programação Python para realizar cálculos simples em problemas de engenharia. Os exemplos a seguir ilustram como usar os tipos de dados, operadores aritméticos e entrada/saída para resolver tarefas comuns em diferentes disciplinas da engenharia.

2.4.1. Engenharia Civil: Cálculo da Área de uma Viga

Problema: Calcular a área da seção transversal de uma viga retangular. Fórmula: Área = base * altura Código Python:

# Entrada de dados
base = float(input("Digite a base da viga (m): "))
altura = float(input("Digite a altura da viga (m): "))

# Cálculo da área
area = base * altura

# Saída de dados
print(f"A área da seção transversal da viga é: {area:.2f} m²")

Resultado:

Digite a base da viga (m): 0.3
Digite a altura da viga (m): 0.5
A área da seção transversal da viga é: 0.15 m²

2.4.2. Engenharia Elétrica: Lei de Ohm

Problema: Calcular a corrente elétrica em um resistor dado a tensão e a resistência. Fórmula: Corrente = Tensão / Resistência Código Python:

# Entrada de dados
tensao = float(input("Digite a tensão (V): "))
resistencia = float(input("Digite a resistência (Ω): "))

# Cálculo da corrente
corrente = tensao / resistencia

# Saída de dados
print(f"A corrente elétrica é: {corrente:.2f} A")

Resultado:

A corrente elétrica é: 2.00 A

2.4.3. Engenharia Mecânica: Energia Potencial Gravitacional

Problema: Calcular a energia potencial gravitacional de um objeto. Fórmula: Energia Potencial = massa * gravidade * altura Código Python:

# Entrada de dados
massa = float(input("Digite a massa do objeto (kg): "))
gravidade = 9.81  # Aceleração da gravidade (m/s²)
altura = float(input("Digite a altura (m): "))
# Cálculo da energia potencial
energia_potencial = massa * gravidade * altura
# Saída de dados
print(f"A energia potencial gravitacional é: {energia_potencial:.2f} J")

Resultado:

Digite a massa do objeto (kg): 10
Digite a altura (m): 5
A energia potencial gravitacional é: 490.50 J

2.4.4. Engenharia Química: Vazão Molar

Problema: Converter vazão mássica para vazão molar. Fórmula: Vazão Molar = Vazão Mássica / Massa Molar Código Python:

# Entrada de dados
vazao_massica = float(input("Digite a vazão mássica (kg/s): "))
massa_molar = float(input("Digite a massa molar (kg/mol): "))

# Cálculo da vazão molar
vazao_molar = vazao_massica / massa_molar

# Saída de dados
print(f"A vazão molar é: {vazao_molar:.2f} mol/s")

Resultado:

A vazão molar é: 2.00 mol/s

2.4.5. Engenharia Ambiental: Cálculo de Concentração

Problema: Calcular a concentração de um poluente em uma solução. Fórmula: Concentração = Massa do Poluente / Volume da Solução Código Python:

# Entrada de dados
massa_poluente = float(input("Digite a massa do poluente (kg): "))
volume_solucao = float(input("Digite o volume da solução (m³): "))

# Cálculo da concentração
concentracao = massa_poluente / volume_solucao

# Saída de dados
print(f"A concentração do poluente é: {concentracao:.2f} kg/m³")

Resultado:

Digite a massa do poluente (kg): 0.5
Digite o volume da solução (m³): 2
A concentração do poluente é: 0.25 kg/m³

2.5. Conclusão

Estes exemplos demonstram como os conceitos básicos de Python podem ser aplicados para resolver problemas simples em diferentes áreas da engenharia. Eles reforçam a importância de: - Entender os tipos de dados apropriados para representar grandezas físicas. - Utilizar os operadores aritméticos corretamente para realizar os cálculos. - Interagir com o usuário para obter os dados necessários e apresentar os resultados de forma clara. Nos próximos módulos, exploraremos conceitos mais avançados de Python para resolver problemas de engenharia mais complexos.

3. Estrutura de Controle

Neste módulo sobre estrutura de controle, exploramos os tipos de dados, operadores e entrada/saída, que nos permitem realizar cálculos e interagir com o usuário. No entanto, a capacidade de um programa de tomar decisões e repetir ações é fundamental para resolver problemas mais complexos. É aqui que entram as estruturas de controle. Este módulo é dedicado ao estudo das estruturas de controle em Python, que são ferramentas essenciais para direcionar o fluxo de execução de um programa. Vamos nos aprofundar em como controlar quais partes do código são executadas e quantas vezes, com base em condições específicas. Primeiramente, abordaremos as condicionais (IF, ELIF, ELSE). As condicionais permitem que o programa escolha diferentes caminhos de execução, dependendo se uma determinada condição é verdadeira ou falsa. Isso é crucial para implementar a lógica de decisão em problemas de engenharia, como verificar se um sensor excedeu um limite de segurança ou classificar dados de acordo com critérios específicos. Em seguida, exploraremos os laços de repetição (FOR, WHILE). Os laços de repetição nos permitem executar um bloco de código repetidamente, até que uma condição seja satisfeita. Isso é extremamente útil para automatizar tarefas repetitivas, como iterar sobre conjuntos de dados, realizar cálculos iterativos ou simular o comportamento de sistemas ao longo do tempo. Finalmente, demonstraremos aplicações práticas em verificação de condições operacionais. Através de exemplos relevantes para a engenharia, mostraremos como as estruturas de controle podem ser usadas para monitorar processos, garantir a segurança de sistemas e automatizar a tomada de decisões em tempo real. Ao concluir este módulo, você estará apto a desenvolver programas Python que não apenas realizam cálculos, mas também tomam decisões lógicas e executam ações repetitivas, abrindo caminho para a criação de soluções de engenharia mais robustas e inteligentes.

3.1. Condicionais: if, elif, else

As estruturas condicionais são fundamentais para controlar o fluxo de execução de um programa, permitindo que diferentes blocos de código sejam executados dependendo se uma condição é verdadeira ou falsa. Em Python, as palavras-chave if, elif (abreviação de “else if”) e else são usadas para definir essas estruturas.

3.1.1. A estrutura if

A estrutura if é a mais básica e executa um bloco de código somente se uma condição especificada for verdadeira.

Sintaxe:

if condição:
    # bloco de código a ser executado se a condição for verdadeira
    pass

Funcionamento: - A condição é uma expressão que pode ser avaliada como True (verdadeiro) ou False (falso). - Se a condição for True, o bloco de código indentado abaixo do if é executado. - Se a condição for False, o bloco de código é ignorado e o programa continua a execução na próxima linha após o bloco if.

• Exemplo em engenharia: Verificar se a temperatura de um sistema excedeu um limite de segurança.

Código Python:

indice_poluicao = float(input("Digite o índice de poluição do ar: "))

if indice_poluicao <= 50:
    print("Qualidade do ar: Boa")
elif indice_poluicao <= 100:
    print("Qualidade do ar: Moderada")
elif indice_poluicao <= 150:
    print("Qualidade do ar: Insatisfatória")
elif indice_poluicao <= 200:
    print("Qualidade do ar: Ruim")
else:
    print("Qualidade do ar: Muito Ruim")

Resultado:

Digite o índice de poluição do ar: 75
Qualidade do ar: Moderada

3.1.2. A estrutura if-else

A estrutura if-else permite executar um bloco de código se a condição for verdadeira e outro bloco de código se a condição for falsa. Sintaxe:

if condição:
    # bloco de código a ser executado se a condição for verdadeira
    pass
else:
    # bloco de código a ser executado se a condição for falsa
    pass

Funcionamento: - A condição é avaliada. - Se a condição for True, o bloco de código do if é executado. - Se a condição for False, o bloco de código do else é executado. - Apenas um dos blocos de código (o do if ou o do else) é executado.

• Exemplo em engenharia: Classificar um material como “resistente” ou “não resistente” com base em um teste de tensão.

Código Python:

tensao = float(input("Digite a tensão aplicada (N/m²): "))
limite = 100.0

if tensao > limite:
    print("Material não resistente.")
else:
    print("Material resistente.")

Resultado:

Digite a tensão aplicada (N/m²): 75
Material resistente.

3.1.3. A estrutura if-elif-else

A estrutura if-elif-else permite verificar múltiplas condições em sequência. O elif (else if) especifica uma nova condição a ser verificada se a condição anterior for falsa.

Sintaxe:

if condição1:
    # bloco de código a ser executado se condição1 for verdadeira
    pass
elif condição2:
    # bloco de código a ser executado se condição2 for verdadeira
    pass
else:
    # bloco de código a ser executado se nenhuma das condições anteriores for verdadeira
    pass

Funcionamento: - As condições são avaliadas em ordem. - Se uma condição for True, o bloco de código correspondente é executado e o restante da estrutura (elif e else) é ignorado. - Se nenhuma condição for True, o bloco de código do else (se houver) é executado. - Pode haver qualquer número de blocos elif. O bloco else é opcional.

Exemplo em engenharia: Classificar a qualidade do ar com base no índice de poluição.

Código Python:

indice_poluicao = float(input("Digite o índice de poluição do ar: "))

if indice_poluicao <= 50:
    print("Qualidade do ar: Boa")
elif indice_poluicao <= 100:
    print("Qualidade do ar: Moderada")
elif indice_poluicao <= 150:
    print("Qualidade do ar: Insatisfatória")
elif indice_poluicao <= 200:
    print("Qualidade do ar: Ruim")
else:
    print("Qualidade do ar: Muito Ruim")

Resultado:

Digite o índice de poluição do ar: 75
Qualidade do ar: Moderada

Pontos-chave: - Indentação: A indentação é crucial em Python para definir os blocos de código dentro das estruturas condicionais. O código dentro de um bloco if, elif ou else deve ser indentado. - Operadores Lógicos: As condições nas estruturas condicionais geralmente envolvem operadores lógicos (and, or, not) e operadores de comparação (==, !=, >, <, >=, <=). - Flexibilidade: As estruturas condicionais podem ser aninhadas (uma dentro da outra) para criar lógicas de decisão mais complexas. Compreender e aplicar corretamente as estruturas condicionais é essencial para desenvolver programas que resolvam problemas reais de engenharia, onde a tomada de decisões é uma parte fundamental do processo.

3.1.4. Exercício Proposto: Classificação de Solos

Descrição: Um engenheiro civil precisa de um programa para classificar amostras de solo com base em seu Índice de Plasticidade (IP) e Limite de Liquidez (LL). O programa deve solicitar ao usuário os valores de IP e LL e exibir a classificação do solo de acordo com a tabela a seguir:

Requisitos:

1. Entrada de Dados:
   • O programa deve solicitar ao usuário o Limite de Liquidez (LL) do solo (FLOAT).
   • O programa deve solicitar ao usuário o Índice de Plasticidade (IP) do solo (FLOAT).
2. Classificação:
   • Utilizar estruturas condicionais (IF, ELIF, ELSE) para classificar o solo de acordo com a tabela fornecida.
3. Saída de Dados:
   • Exibir o Limite de Liquidez (LL) e o Índice de Plasticidade (IP) inseridos pelo usuário, formatados com duas casas decimais.
   • Exibir a classificação do solo.

Exemplo de Interação:

Digite o Limite de Liquidez (LL) do solo: 45
Digite o Índice de Plasticidade (IP) do solo: 25
Limite de Liquidez (LL): 45.00
Índice de Plasticidade (IP): 25.00
Classificação do Solo: Solo Argiloso

Dicas:

• Use a função input() para obter os valores de LL e IP do usuário.
• Use os tipos de dados FLOAT para armazenar os valores de LL e IP.
• Lembre-se de converter as entradas de input() para FLOAT.
• Use os operadores de comparação (>=, <, ==) e os operadores lógicos (AND, OR, NOT) para implementar as condições de classificação.
• Use f-strings para formatar a saída com duas casas decimais.

Código Python:

# Entrada de dados
ll = float(input("Digite o Limite de Liquidez (LL): "))
ip = float(input("Digite o Índice de Plasticidade (IP): "))

# Classificação do solo
if ll >= 50 and ip >= 7:
    classificacao = "Argila"
elif ll < 50 and 4 <= ip < 7:
    classificacao = "Silte"
else:
    classificacao = "Solo Não Plástico"

# Saída de dados
print(f"\nLimite de Liquidez (LL): {ll:.2f}")
print(f"Índice de Plasticidade (IP): {ip:.2f}")
print(f"Classificação do Solo: {classificacao}")

Resultado:

Limite de Liquidez (LL): 45.00
Índice de Plasticidade (IP): 25.00
Classificação do Solo: Solo Argiloso

Este exercício aplica as estruturas condicionais em um problema prático de engenharia civil, demonstrando como a lógica de decisão pode ser implementada em programas para classificar dados e auxiliar na análise de materiais.

3.1.5. Curiosidade – Engenharia Civil

Na engenharia civil, a classificação de solos é uma etapa crucial no projeto e construção de fundações, estradas e outras estruturas. A tabela de classificação de solos baseada no Índice de Plasticidade (IP) e Limite de Liquidez (LL) é amplamente utilizada para entender as propriedades mecânicas do solo. A classificação de solos é baseada em normas técnicas, como a ASTM D2487, que define os critérios para categorizar solos em diferentes grupos, como argilas, siltes e solos não plásticos. Esses grupos são importantes porque influenciam diretamente o comportamento do solo sob carga, sua capacidade de suporte e sua suscetibilidade à deformação. A tabela de classificação apresentada no exercício é uma simplificação, mas reflete os princípios básicos usados na prática. A classificação correta do solo é essencial para garantir a segurança e a estabilidade das estruturas construídas sobre ele.

3.1.6. Conclusão

Dominar as estruturas condicionais IF, ELIF e ELSE é um marco importante na jornada de programação. Elas fornecem a base para criar programas que não apenas executam cálculos, mas também respondem dinamicamente a diferentes entradas e condições. Nos próximos itens e módulos, veremos como essa habilidade será aplicada em contextos mais complexos, como laços de repetição, funções e projetos de engenharia.

3.2. Laços de Repetição: for, while

Os laços de repetição são fundamentais na programação, permitindo que um bloco de código seja executado várias vezes, com base em uma condição. Em Python, os principais tipos de laços são o for e o while.

O laço for é usado para iterar sobre uma sequência (como uma lista, tupla ou string) e executar um bloco de código para cada item da sequência. A sintaxe básica é:

for item in sequencia:
    # bloco de código

O laço while, por outro lado, executa um bloco de código enquanto uma condição específica for verdadeira. A sintaxe básica é:

while condicao:
    # bloco de código

Ambos os tipos de laços são amplamente utilizados em problemas de engenharia, como simulações, otimizações e análises de dados.

3.2.1. O laço for

Os laços de repetição são estruturas de controle que permitem executar um bloco de código repetidamente, um número específico de vezes ou enquanto uma condição for verdadeira. Em Python, os dois tipos principais de laços são FOR e WHILE. O laço for é usado para iterar sobre uma sequência (como uma lista, tupla ou string) e executar um bloco de código para cada item da sequência. A sintaxe básica é:

for item in sequencia:
    # bloco de código

Funcionamento: - A variável item assume o valor de cada elemento da sequencia a cada iteração. - O bloco de código indentado abaixo do for é executado para cada item. - O laço termina quando todos os itens da sequência foram processados. Exemplo em engenharia: Calcular a média de uma série de medidas de temperatura.

temperaturas = [20.5, 22.0, 19.8, 21.5, 23.0]
soma_temperaturas = 0.0
for temperatura in temperaturas:
    soma_temperaturas += temperatura
media_temperatura = soma_temperaturas / len(temperaturas)
print(f"Média de temperatura: {media_temperatura:.2f} °C")

Resultado:

Média de temperatura: 21.16 °C

3.2.2. O laço while

O laço while executa um bloco de código enquanto uma condição específica for verdadeira. É útil quando o número de iterações não é conhecido previamente.

Sintaxe:

while condicao:
    # bloco de código

Funcionamento: - A condição é avaliada antes de cada iteração. - Se a condição for True, o bloco de código indentado é executado. - Após a execução do bloco, a condição é verificada novamente. - O laço continua até que a condição se torne False.

Exemplos em engenharia: Iterar sobre uma lista de medições de temperatura:

Calcular a soma dos quadrados dos 10 primeiros números inteiros:

soma_quadrados = 0
contador = 1
while contador <= 10:
    soma_quadrados += contador**2
    contador += 1
print(f"Soma dos quadrados: {soma_quadrados}")

Funcionamento: - A condição é avaliada antes de cada iteração. - Se a condição for True, o bloco de código indentado é executado. - Após a execução do bloco, a condição é verificada novamente. - O laço continua até que a condição se torne False.

Exemplo em engenharia: Simular o resfriamento de um líquido até atingir uma temperatura segura.

temperatura = 100.0  # Temperatura inicial em °C
while temperatura > 30.0:  # Condição de resfriamento
    print(f"Temperatura atual: {temperatura:.2f} °C")
    temperatura -= 5.0  # Resfriamento de 5 °C por iteração
print("Temperatura segura alcançada.")

Resultado:

Temperatura atual: 100.00 °C
Temperatura atual: 95.00 °C
Temperatura atual: 90.00 °C
Temperatura atual: 85.00 °C
Temperatura atual: 80.00 °C
Temperatura atual: 75.00 °C
Temperatura atual: 70.00 °C
Temperatura atual: 65.00 °C
Temperatura atual: 60.00 °C
Temperatura atual: 55.00 °C
Temperatura atual: 50.00 °C
Temperatura atual: 45.00 °C
Temperatura atual: 40.00 °C
Temperatura atual: 35.00 °C
Temperatura segura alcançada.

Pontos-chave: - Controle de Iteração: O laço for é ideal quando se sabe o número de iterações ou quando se está iterando sobre uma sequência. O laço while é mais flexível, permitindo que o número de iterações dependa de uma condição dinâmica. - Condição de Parada: É crucial definir uma condição de parada para os laços while para evitar laços infinitos (onde o laço nunca termina). - Variáveis de Controle: As variáveis usadas nas condições dos laços (como contador, temperatura, etc.) devem ser atualizadas dentro do laço para garantir que a condição de parada seja eventualmente alcançada. - range(): A função range() é frequentemente usada com o laço for para gerar sequências de números. Por exemplo, for i in range(10): itera de 0 a 9.

Os laços de repetição são ferramentas poderosas para automatizar tarefas, processar grandes conjuntos de dados e implementar algoritmos iterativos em diversas aplicações de engenharia. Eles permitem que os engenheiros desenvolvam soluções eficientes e escaláveis para problemas complexos, economizando tempo e esforço no desenvolvimento de software.

3.2.3. Exercício Proposto: Simulação de um Reator Batelada Isotérmico

Descrição: Um engenheiro químico precisa simular a conversão de um reagente A em um produto B em um reator batelada isotérmico. A reação segue uma cinética de primeira ordem:

Reação: A → B

A taxa de reação é dada por:

- rA = -k * CA

Onde: - -rA é a taxa de desaparecimento do reagente A (mol/L·min) - k é a constante de velocidade da reação (min⁻¹) - CA é a concentração do reagente A (mol/L)

O programa deve calcular a concentração de A e a conversão de A ao longo do tempo.

Requisitos:

1. Entrada de Dados:

• O programa deve solicitar ao usuário a concentração inicial de A (CA0) em mol/L (FLOAT).
• O programa deve solicitar ao usuário a constante de velocidade da reação (k) em min⁻¹ (FLOAT).
• O programa deve solicitar ao usuário o tempo total de simulação (tempo_final) em minutos (FLOAT).
• O programa deve solicitar ao usuário o número de pontos no tempo para calcular a concentração (num_pontos) (INT).

2. Cálculos:

• Usar um laço for para iterar sobre o tempo, dividindo o tempo total em intervalos iguais.
• Dentro do laço, calcular a concentração de A (CA) em cada ponto no tempo usando a equação integrada para uma reação de primeira ordem em um reator batelada:

CA(t) = CA0 * exp(-k * t)

import math

# Entrada de Dados
CA0 = float(input("Concentração inicial de A (CA0) em mol/L: "))
k = float(input("Constante de velocidade da reação (k) em min⁻¹: "))
tempo_final = float(input("Tempo total de simulação (tempo_final) em minutos: "))
num_pontos = int(input("Número de pontos no tempo para calcular a concentração (num_pontos): "))

# Cálculos
tempos = []
concentracoes_A = []
for i in range(num_pontos + 1):
    t = i * (tempo_final / num_pontos)  # Tempo atual
    CA = CA0 * math.exp(-k * t)  # Cálculo da concentração de A
    tempos.append(t)
    concentracoes_A.append(CA)

# Exibição dos resultados
for i in range(len(tempos)):
    print(f"Tempo: {tempos[i]:.1f} min, [A]: {concentracoes_A[i]:.2f} mol/L, [B]: {1 - concentracoes_A[i]:.2f} mol/L")

Saída de Dados:

Concentração inicial de A (CA0) em mol/L: 1.0
Constante de velocidade da reação (k) em min⁻¹: 0.1
Tempo total de simulação (tempo_final) em minutos: 10
Número de pontos no tempo para calcular a concentração (num_pontos): 10
Tempo: 0.0 min, [A]: 1.00 mol/L, [B]: 0.00 mol/L
Tempo: 1.0 min, [A]: 0.90 mol/L, [B]: 0.10 mol/L
Tempo: 2.0 min, [A]: 0.82 mol/L, [B]: 0.18 mol/L
Tempo: 3.0 min, [A]: 0.74 mol/L, [B]: 0.26 mol/L
Tempo: 4.0 min, [A]: 0.67 mol/L, [B]: 0.33 mol/L
Tempo: 5.0 min, [A]: 0.61 mol/L, [B]: 0.39 mol/L
Tempo: 6.0 min, [A]: 0.55 mol/L, [B]: 0.45 mol/L
Tempo: 7.0 min, [A]: 0.50 mol/L, [B]: 0.50 mol/L
Tempo: 8.0 min, [A]: 0.45 mol/L, [B]: 0.55 mol/L
Tempo: 9.0 min, [A]: 0.41 mol/L, [B]: 0.59 mol/L
Tempo: 10.0 min, [A]: 0.37 mol/L, [B]: 0.63 mol/L

Este exercício simula um processo fundamental em engenharia química (reação em reator) e demonstra o uso de laços for para realizar cálculos iterativos ao longo do tempo.

Dicas: - Use a função input() para obter os valores de CA0, k, tempo_final e num_pontos do usuário. - Use os tipos de dados FLOAT para CA0, k e tempo_final, e INT para num_pontos. - Use a função math.exp() para calcular a exponencial na equação da concentração de A. - Use um laço for para iterar sobre o número de pontos no tempo e calcular a concentração de A em cada ponto. - Use f-strings para formatar a saída com duas casas decimais.

3.2.4. Curiosidade – Engenharia Química

Na engenharia química, a simulação de reatores é uma prática comum para entender o comportamento de reações químicas em diferentes condições. O exemplo apresentado no exercício propõe uma simulação de um reator batelada isotérmico, onde a concentração de um reagente A diminui ao longo do tempo devido à reação com uma constante de velocidade k. A cinética de primeira ordem é uma das mais simples e comuns em reações químicas, onde a taxa de reação é proporcional à concentração do reagente. A equação integrada para a concentração de A ao longo do tempo é fundamental para prever como a reação evolui, permitindo aos engenheiros otimizar as condições de operação do reator. A simulação de reatores é essencial para o design e operação de processos químicos, ajudando a prever a conversão de reagentes, a formação de produtos e a eficiência do processo. Compreender como implementar laços de repetição em Python para simular essas dinâmicas é uma habilidade valiosa para engenheiros químicos.

3.2.5. Conclusão

Os laços de repetição for e while são ferramentas poderosas na programação, permitindo a execução de blocos de código múltiplas vezes com base em condições específicas. Eles são amplamente utilizados em problemas de engenharia para automatizar tarefas, processar dados e simular comportamentos dinâmicos. Compreender como usar esses laços é essencial para desenvolver programas eficientes e eficazes. Nos próximos módulos, veremos como combinar laços de repetição com outras estruturas de controle, como condicionais e funções, para criar soluções mais complexas e robustas em Python.

3.3. Aplicações Práticas em Verificação de Condições Operacionais

As estruturas de controle (IF, ELIF, ELSE, FOR, WHILE) são extremamente úteis para monitorar e controlar condições operacionais em sistemas de engenharia. Nesta seção, apresentaremos exemplos práticos de como essas estruturas podem ser aplicadas para garantir a segurança, eficiência e correto funcionamento de processos e equipamentos.

3.3.1. Monitoramento de Temperatura em um Reator Químico

Em um reator químico, a temperatura é um parâmetro crítico que deve ser mantido dentro de limites seguros para evitar reações indesejadas ou danos ao equipamento. O código abaixo demonstra como usar condicionais para verificar a temperatura e emitir alertas:

Código Python:

temperatura = float(input("Digite a temperatura do reator em °C: "))
if temperatura > 100:
    print("Alerta: Temperatura excessiva!")
elif temperatura < 20:
    print("Alerta: Temperatura muito baixa!")
else:
    print("Temperatura dentro dos limites normais.")

Resultado:

Digite a temperatura do reator em °C: 120
Alerta: Temperatura excessiva!
Digite a temperatura do reator em °C: 15
Alerta: Temperatura muito baixa!
Digite a temperatura do reator em °C: 50
Temperatura dentro dos limites normais.

3.3.2. Controle de Nível em um Tanque

O nível de líquido em um tanque é outro parâmetro importante em muitos processos industriais. O código a seguir ilustra como usar condicionais para controlar o nível e acionar bombas ou válvulas:

Código Python:

nivel = float(input("Digite o nível do líquido no tanque em %: "))
if nivel > 80:
    print("Alerta: Nível muito alto! Acionando bomba de drenagem.")
elif nivel < 20:
    print("Alerta: Nível muito baixo! Acionando bomba de enchimento.")
else:
    print("Nível dentro dos limites normais.")

Resultado:

Digite o nível do líquido no tanque em %: 85
Alerta: Nível muito alto! Acionando bomba de drenagem.
Digite o nível do líquido no tanque em %: 15
Alerta: Nível muito baixo! Acionando bomba de enchimento.
Digite o nível do líquido no tanque em %: 50
Nível dentro dos limites normais.

3.3.3. Verificação de Pressão em um Sistema de Tubulação

A pressão em um sistema de tubulação deve ser monitorada para evitar vazamentos ou rupturas. O código abaixo mostra como usar condicionais para verificar a pressão e emitir avisos:

Código Python:

pressao = float(input("Digite a pressão do sistema em bar: "))
if pressao > 10:
    print("Alerta: Pressão excessiva!")
elif pressao < 2:
    print("Alerta: Pressão muito baixa!")
else:
    print("Pressão dentro dos limites normais.")

Resultado:

Digite a pressão do sistema em bar: 12
Alerta: Pressão excessiva!
Digite a pressão do sistema em bar: 1
Alerta: Pressão muito baixa!
Digite a pressão do sistema em bar: 5
Pressão dentro dos limites normais.

3.3.4. Contagem de Ciclos de um Equipamento

Em engenharia mecânica, é importante monitorar o número de ciclos de operação de um equipamento para programar a manutenção preventiva. O código a seguir usa um laço WHILE para simular a operação de um equipamento e contar os ciclos:

Código Python:

ciclos = 0
while True:
    resposta = input("O equipamento está em operação? (s/n): ")
    if resposta == "s":
        ciclos += 1
        print(f"Ciclos de operação: {ciclos}")
    elif resposta == "n":
        print("Operação encerrada.")
        break
    else:
        print("Resposta inválida.")

Resultado:

O equipamento está em operação? (s/n): s
Ciclos de operação: 1
O equipamento está em operação? (s/n): s
Ciclos de operação: 2
O equipamento está em operação? (s/n): n
Operação encerrada.

3.3.5. Análise de Dados de Sensores

Em sistemas de automação, os dados dos sensores precisam ser analisados para tomar decisões em tempo real. O código a seguir usa um laço for para processar dados de um sensor de vibração e identificar valores anormais:

Código Python:

dados_sensor = [0.1, 0.2, 0.15, 0.3, 0.25, 0.4]
for i, valor in enumerate(dados_sensor):
    if valor > 0.35:
        print(f"Alerta: Valor anormal detectado no ciclo {i + 1}: {valor}")
    else:
        print(f"Ciclo {i + 1} dentro dos limites normais: {valor}")

Resultado:

Ciclo 1 dentro dos limites normais: 0.1
Ciclo 2 dentro dos limites normais: 0.2
Ciclo 3 dentro dos limites normais: 0.15
Ciclo 4 dentro dos limites normais: 0.3
Alerta: Valor anormal detectado no ciclo 5: 0.25
Alerta: Valor anormal detectado no ciclo 6: 0.4

Estes exemplos demonstram a versatilidade das estruturas de controle na verificação de condições operacionais em diversos campos da engenharia. Ao utilizar IF, ELIF, ELSE, FOR e WHILE, os engenheiros podem criar programas que monitoram sistemas, detectam anomalias, acionam alarmes e automatizam ações de controle, contribuindo para a segurança, eficiência e confiabilidade dos processos e equipamentos.

3.4. Conclusão

Neste módulo, exploramos as estruturas de controle em Python, incluindo condicionais (IF, ELIF, ELSE) e laços de repetição (FOR, WHILE). Aprendemos como essas estruturas permitem que os programas tomem decisões lógicas e executem ações repetitivas, fundamentais para resolver problemas complexos em engenharia. Através de exemplos práticos, vimos como aplicar essas estruturas para monitorar condições operacionais, controlar processos e automatizar tarefas. A compreensão e aplicação correta dessas estruturas são essenciais para desenvolver programas eficientes e eficazes em diversas áreas da engenharia. Nos próximos módulos, continuaremos a explorar conceitos mais avançados de Python, como funções, manipulação de dados e bibliotecas específicas para engenharia, que nos permitirão criar soluções ainda mais robustas e complexas. A prática contínua com estruturas de controle fortalecerá suas habilidades de programação e sua capacidade de resolver problemas reais de engenharia.

4. Funções e Modularizações

Neste módulo 4, vamos explorar dois conceitos fundamentais para a organização e reutilização de código em Python: funções e modularização. Primeiramente, abordaremos a definição de funções. Funções são blocos de código nomeados que realizam tarefas específicas. Aprenderemos a criar nossas próprias funções para encapsular a lógica de cálculos, processos ou outras operações que precisam ser executadas repetidamente em um programa. Isso evita a duplicação de código e torna os programas mais legíveis e fáceis de manter. Em seguida, discutiremos parâmetros e retorno. Veremos como as funções podem receber dados de entrada através de parâmetros, permitindo que elas operem sobre diferentes valores. Também aprenderemos como as funções podem retornar resultados, possibilitando que elas forneçam informações para outras partes do programa. O uso adequado de parâmetros e retorno é essencial para criar funções flexíveis e reutilizáveis. Finalmente, exploraremos a organização de código em módulos reutilizáveis. A modularização envolve a divisão de um programa em arquivos separados chamados módulos. Cada módulo pode conter funções, variáveis e outras definições relacionadas a uma funcionalidade específica. Aprenderemos a criar e importar módulos, o que nos permitirá estruturar projetos maiores de forma eficiente e reutilizar código entre diferentes programas. Ao concluir este módulo, você estará apto a criar funções para organizar seu código, usar parâmetros e retorno para torná-las flexíveis e estruturar projetos em módulos para promover a reutilização e a manutenção eficiente do código, habilidades cruciais para o desenvolvimento de soluções de engenharia robustas e escaláveis.

4.1. Definição de Funções

Em Python, uma função é um bloco de código organizado e reutilizável que executa uma tarefa específica. Funções ajudam a dividir programas complexos em partes menores e gerenciáveis, tornando o código mais legível, organizado e fácil de manter. As funções são definidas usando a palavra-chave def, seguida pelo nome da função e parênteses que podem conter parâmetros. O corpo da função é indentado abaixo da definição e contém o código que será executado quando a função for chamada.

4.1.1. Sintaxe de Definição de Função

A sintaxe para definir uma função em Python é a seguinte:

def nome_da_funcao(parametros):
    # bloco de código a ser executado
    pass

Componentes: - def: palavra-chave que indica o início da definição de uma função. - nome_da_funcao: o nome da função, que deve ser descritivo e seguir as convenções de nomenclatura do Python. - parametros: uma lista de variáveis que a função pode receber como entrada (opcional). - pass: um comando que indica que a função não faz nada (pode ser substituído pelo código real da função).

4.1.2. Exemplo de Definição de Função

Vamos criar uma função simples que calcula a área de um retângulo. A função receberá dois parâmetros: a base e a altura do retângulo, e retornará a área calculada.

def calcular_area_retangulo(base, altura):
    area = base * altura
    return area
# Chamada da função
area = calcular_area_retangulo(5, 10)
print(f"A área do retângulo é: {area} m²")

Resultado:

A área do retângulo é: 50 m²

4.1.3. Benefícios do Uso de Funções

As funções oferecem vários benefícios importantes na programação, especialmente em engenharia:

• Reutilização de código: Funções permitem que você execute o mesmo bloco de código várias vezes sem precisar reescrevê-lo.
• Organização do código: Funções ajudam a dividir programas grandes em partes menores e mais gerenciáveis, tornando o código mais fácil de entender e manter.
• Legibilidade do código: Funções tornam o código mais legível, pois dão nomes significativos a blocos de código, facilitando a compreensão do que cada parte do programa faz.
• Facilidade de manutenção: Se você precisar modificar o comportamento de uma parte específica do código, basta alterar a função correspondente, em vez de procurar e alterar o mesmo código em vários lugares.

No contexto da engenharia, as funções podem ser usadas para encapsular cálculos complexos, simulações, análises de dados e outras tarefas comuns, promovendo a eficiência e a clareza no desenvolvimento de software.

4.2. Parâmetros e Retorno

Parâmetros e retorno são mecanismos que permitem que as funções se comuniquem com o “mundo exterior”, ou seja, que recebam dados para trabalhar e que forneçam resultados de volta para quem as chamou.

4.2.1. Parâmetros

Os parâmetros são variáveis que você define na declaração da função e que permitem que a função receba valores de entrada quando é chamada. Eles são especificados entre parênteses na definição da função.

Sintaxe:

def nome_da_funcao(parametro1, parametro2):
    # bloco de código a ser executado
    pass

1. Tipos de Parâmetros:

Parâmetros Posicionais: São os mais comuns. A ordem em que você passa os valores ao chamar a função deve corresponder à ordem em que os parâmetros são definidos na função.

Parâmetros Nomeados (ou Palavra-Chave): Ao chamar a função, você especifica o nome do parâmetro seguido do valor. Isso permite passar os argumentos em qualquer ordem.

Parâmetros com Valores Padrão: Você pode fornecer valores padrão para os parâmetros. Se um valor não for fornecido ao chamar a função, o valor padrão será usado.

Número Variável de Argumentos: Você pode definir funções que aceitam um número variável de argumentos usando *args e **kwargs.

2. Exemplos de Parâmetros:

def exemplo_args(*args):
    for i in args:
        print(i)

def exemplo_kwargs(**kwargs):
    for chave, valor in kwargs.items():
        print(f"{chave}: {valor}")

# Chamada da função com parâmetros posicionais
exemplo_args(1, 2, 3, 4)
# Chamada da função com parâmetros nomeados
exemplo_kwargs(nome="João", idade=30, cidade="São Paulo")

4.2.2. Retorno

O retorno é o mecanismo pelo qual uma função envia um resultado de volta para quem a chamou. Você pode usar a palavra-chave return para especificar o valor que a função deve retornar.

Sintaxe:

def nome_da_funcao(parametros):
    # bloco de código a ser executado
    return valor_de_retorno

Exemplo de Retorno:

def calcular_media(notas):
    soma = sum(notas)
    media = soma / len(notas)
    return media
# Chamada da função
notas = [7.5, 8.0, 6.5, 9.0]
media = calcular_media(notas)
print(f"A média das notas é: {media:.2f}")

Resultado:

A média das notas é: 7.75

Importância: Parâmetros tornam as funções flexíveis e reutilizáveis, permitindo que operem em diferentes dados. O retorno permite que as funções produzam resultados que podem ser usados em outras partes do programa. Juntos, parâmetros e retorno são cruciais para a criação de funções modulares e eficientes.

4.2.3. Benefícios de Parâmetros e Retorno

Parâmetros e retorno oferecem vários benefícios importantes na programação, especialmente em engenharia: - Flexibilidade: Permitem que as funções operem em diferentes dados, tornando-as reutilizáveis em várias situações. - Modularidade: Facilitam a criação de funções que podem ser combinadas para resolver problemas complexos, promovendo a organização do código. - Clareza: A utilização de parâmetros nomeados torna o código mais legível, pois deixa claro o propósito de cada argumento passado para a função. - Eficiência: Permitem que as funções retornem resultados que podem ser usados imediatamente, evitando a necessidade de variáveis globais ou estados compartilhados. - Testabilidade: Funções com parâmetros e retorno são mais fáceis de testar, pois você pode verificar se a função produz os resultados esperados para diferentes entradas. Esses benefícios são essenciais para o desenvolvimento de software de engenharia, onde a clareza, a reutilização e a eficiência do código são fundamentais para resolver problemas complexos e garantir a qualidade das soluções.

4.3. Organização de Código em Módulos Reutilizáveis

A organização de código em módulos reutilizáveis é uma prática fundamental na programação, especialmente em projetos maiores e mais complexos. Módulos permitem que você divida seu código em arquivos separados, cada um contendo funções, classes e variáveis relacionadas a uma funcionalidade específica. Isso promove a reutilização de código, facilita a manutenção e melhora a legibilidade do programa.

4.3.1. O que são Módulos?

Módulos são arquivos Python que contêm definições de funções, classes e variáveis. Eles permitem que você organize seu código em partes lógicas, facilitando a reutilização e a manutenção. Você pode importar módulos em outros arquivos Python para acessar suas funcionalidades.

Exemplo de Módulo:

# meu_modulo.py
def saudacao(nome):
    return f"Olá, {nome}!"

def soma(a, b):
    return a + b
# Variável global
mensagem = "Este é um módulo de exemplo."

4.3.2. Criando Módulos

Para criar um módulo, basta salvar o código Python em um arquivo .py.

Exemplo: Criando um módulo chamado calculos_geometricos.py

# calculos_geometricos.py
def area_circulo(raio):
    import math
    return math.pi * raio**2

def perimetro_circulo(raio):
    import math
    return 2 * math.pi * raio

4.3.3. Importando Módulos

Para usar um módulo em outro arquivo Python, você deve importá-lo. Existem várias maneiras de importar módulos:

1. Importação Simples:

   import meu_modulo
   print(meu_modulo.saudacao("Maria"))

2. Importação Específica:

   from meu_modulo import saudacao
   print(saudacao("Maria"))

3. Importação com Alias:

   import meu_modulo as mm
   print(mm.saudacao("Maria"))

4. Importação de Todas as Funções:

   from meu_modulo import *
   print(saudacao("Maria"))
   print(soma(5, 10))

4.3.4. Benefícios da Modularização

A modularização oferece vários benefícios importantes na programação, especialmente em engenharia: - Reutilização de Código: Módulos permitem que você reutilize funções e classes em diferentes projetos, economizando tempo e esforço. - Organização: Dividir o código em módulos torna mais fácil entender e manter o programa, pois cada módulo pode ser focado em uma funcionalidade específica. - Colaboração: Em projetos maiores, diferentes desenvolvedores podem trabalhar em módulos separados, facilitando a colaboração e a integração do código. - Testabilidade: Módulos podem ser testados individualmente, o que facilita a identificação de bugs e a validação do comportamento esperado. - Escalabilidade: Módulos permitem que você expanda seu código de forma organizada, adicionando novas funcionalidades sem comprometer a estrutura existente. Esses benefícios são essenciais para o desenvolvimento de software de engenharia, onde a clareza, a reutilização e a eficiência do código são fundamentais para resolver problemas complexos e garantir a qualidade das soluções.

4.3.5. Exemplo de Uso de Módulos

import geometria

raio = 5
base = 4
altura = 3

print(f"Área do círculo: {geometria.area_circulo(raio):.2f} m²")
print(f"Perímetro do círculo: {geometria.perimetro_circulo(raio):.2f} m")
print(f"Área do retângulo: {geometria.area_retangulo(base, altura)} m²")
print(f"Perímetro do retângulo: {geometria.perimetro_retangulo(base, altura)} m")

Vamos criar um exemplo prático que utiliza módulos para calcular áreas e perímetros de formas geométricas. Primeiro, criaremos um módulo chamado geometria.py que conterá funções para calcular a área e o perímetro de um círculo e um retângulo.

```python# geometria.py import math

def area_circulo(raio): return math.pi * raio**2

def perimetro_circulo(raio): return 2 * math.pi * raio

def area_retangulo(base, altura): return base * altura

def perimetro_retangulo(base, altura): return 2 * (base + altura)

Agora, podemos usar esse módulo em outro arquivo Python para realizar os cálculos. Vamos criar um arquivo chamado `main.py` que importa o módulo `geometria` e utiliza suas funções.

```python
# main.py
import geometria
raio = 5
base = 4
altura = 3
print(f"Área do círculo: {geometria.area_circulo(raio):.2f} m²")
print(f"Perímetro do círculo: {geometria.perimetro_circulo(raio):.2f} m")
print(f"Área do retângulo: {geometria.area_retangulo(base, altura)} m²")
print(f"Perímetro do retângulo: {geometria.perimetro_retangulo(base, altura)} m")

Resultado:

Área do círculo: 78.54 m²
Perímetro do círculo: 31.42 m
Área do retângulo: 12 m²
Perímetro do retângulo: 14 m

Neste exemplo, criamos um módulo geometria.py que contém funções para calcular a área e o perímetro de um círculo e um retângulo. Em seguida, importamos esse módulo no arquivo main.py e utilizamos suas funções para realizar os cálculos necessários. Isso demonstra como a modularização pode tornar o código mais organizado e reutilizável.

4.3.5 Exercício Proposto: Gestão de Inventário Florestal

Descrição:
Um engenheiro florestal precisa desenvolver um sistema para gerenciar o inventário de uma floresta. O sistema deve calcular o volume de madeira em diferentes parcelas, verificar a idade das árvores para determinar o momento ideal de corte e gerar relatórios resumidos. Para organizar o código e facilitar a reutilização, o sistema será estruturado em módulos e funções.

Requisitos: 1. Criar um módulo calculos_florestais.py com funções para calcular o volume de uma árvore, a idade de corte e gerar relatórios. 2. No programa principal, importar o módulo, definir dados de exemplo de uma parcela florestal (lista de dicionários), chamar as funções do módulo e exibir o relatório na tela.

Código do Módulo (calculos_florestais.py):

import math

def calcular_volume(dap, altura, fator_forma=0.7):
    """Calcula o volume de uma árvore."""
    raio = dap / 2 / 100
    volume = math.pi * (raio ** 2) * altura * fator_forma
    return volume

def calcular_idade_corte(especie, crescimento_anual):
    """Calcula a idade estimada de corte para uma árvore."""
    idade_corte = 40 / crescimento_anual
    return int(idade_corte)

def gerar_relatorio(parcela, dados_arvores):
    """Gera um relatório sumarizado da parcela florestal."""
    relatorio = f"Relatório da Parcela: {parcela}\n"
    relatorio += "-----------------------------------\n"
    relatorio += "|  Espécie  | DAP (cm) | Altura (m) | Volume (m³) | Idade Corte (anos) |\n"
    relatorio += "-----------------------------------\n"
    for arvore in dados_arvores:
        volume = calcular_volume(arvore['dap'], arvore['altura'])
        idade_corte = calcular_idade_corte(arvore['especie'], arvore['crescimento_anual'])
        relatorio += f"| {arvore['especie']:<9} | {arvore['dap']:8.2f} | {arvore['altura']:8.2f} | {volume:9.3f} | {idade_corte:16} |\n"
    relatorio += "-----------------------------------\n"
    return relatorio

Programa Principal (main.py):

import calculos_florestais

if __name__ == "__main__":
    dados_parcela = [
        {'especie': 'Eucalipto', 'dap': 15.5, 'altura': 12.0, 'idade': 7, 'crescimento_anual': 2.5},
        {'especie': 'Pinus', 'dap': 22.0, 'altura': 18.0, 'idade': 12, 'crescimento_anual': 1.8},
        {'especie': 'Acacia', 'dap': 10.0, 'altura': 8.5, 'idade': 5, 'crescimento_anual': 3.0}
    ]

    relatorio_parcela = calculos_florestais.gerar_relatorio("Parcela A1", dados_parcela)
    print(relatorio_parcela)

Saída Esperada:

Relatório da Parcela: Parcela A1
-----------------------------------
|  Espécie  | DAP (cm) | Altura (m) | Volume (m³) | Idade Corte (anos) |
-----------------------------------
| Eucalipto |    15.50 |      12.00 |      1.767 |                16 |
| Pinus     |    22.00 |      18.00 |      3.141 |                22 |
| Acacia    |    10.00 |       8.50 |      0.706 |                13 |
-----------------------------------

Este exercício simula um sistema de gestão de inventário florestal, onde o engenheiro florestal pode calcular o volume de madeira, a idade de corte e gerar relatórios sumarizados para diferentes parcelas florestais. A modularização do código permite que as funções sejam reutilizadas em diferentes contextos, promovendo a eficiência e a clareza no desenvolvimento de software de engenharia.

4.4. Conclusão

Neste módulo, mergulhamos nos conceitos de funções e modularização em Python, aprendendo a criar funções para encapsular a lógica de tarefas específicas, a utilizar parâmetros para torná-las flexíveis e a retornar valores para comunicar resultados. Demonstramos como a modularização permite organizar o código em módulos reutilizáveis, facilitando a manutenção, a colaboração e a escalabilidade de projetos. O exemplo prático de gestão de inventário florestal ilustrou a aplicação desses conceitos em um problema real de engenharia, evidenciando como funções e módulos contribuem para o desenvolvimento de soluções mais estruturadas, eficientes e fáceis de manter. O domínio desses conceitos é um passo fundamental para o desenvolvimento de software de alta qualidade em engenharia.

5. Estruturas de Dados

Este módulo apresenta as estruturas de dados fundamentais em Python: listas, tuplas e dicionários. Listas são sequências mutáveis de elementos, úteis para armazenar coleções de itens que podem ser modificados. Tuplas são sequências imutáveis, ideais para representar conjuntos de dados fixos. Dicionários são coleções de pares chave-valor, que permitem acessar dados de forma eficiente através de uma chave. Neste módulo, aprenderemos a criar, acessar, modificar e manipular essas estruturas, bem como a iterar sobre seus elementos para realizar operações diversas. As aplicações em vetores de parâmetros de processo ilustrarão como essas estruturas podem ser usadas para organizar e analisar dados em sistemas de engenharia, como medições de temperatura, pressão e vazão.

5.1. Listas, Tuplas e Dicionários

Python oferece diversas estruturas de dados para organizar e armazenar coleções de dados. As mais fundamentais e amplamente utilizadas são listas, tuplas e dicionários. Cada uma dessas estruturas possui características e usos específicos, tornando-as adequadas para diferentes situações na programação.

5.1.1. Listas

Definição:
Listas são sequências ordenadas de itens. Os itens em uma lista podem ser de qualquer tipo de dado (números, strings, outras listas, etc.) e podem ser modificados após a criação da lista.

Características: - Mutáveis: Você pode adicionar, remover ou alterar elementos de uma lista. - Ordenadas: Os itens em uma lista mantêm uma ordem específica. - Indexadas: Você pode acessar os itens em uma lista usando índices (a posição do item na lista, começando em 0). - Permitem duplicatas: Uma lista pode conter múltiplos itens com o mesmo valor.

Sintaxe:
Listas são criadas usando colchetes [ ] e os itens são separados por vírgulas.

Exemplo de Código em Python:

# Exemplo de criação de uma lista
minha_lista = [1, 2, 3, 4, 5]

# Acessando elementos da lista
print(minha_lista[0])  # Saída: 1
print(minha_lista[2])  # Saída: 3

# Modificando um elemento da lista
minha_lista[1] = 10
print(minha_lista)  # Saída: [1, 10, 3, 4, 5]

# Adicionando um elemento à lista
minha_lista.append(6)
print(minha_lista)  # Saída: [1, 10, 3, 4, 5, 6]

# Removendo um elemento da lista
minha_lista.remove(10)
print(minha_lista)  # Saída: [1, 3, 4, 5, 6]

# Iterando sobre uma lista
for item in minha_lista:
    print(item)

Resultado:

1
3
4
5
6

Aplicação em Engenharia:
Listas são muito úteis para armazenar conjuntos de medições, resultados de experimentos, parâmetros de processos, entre outros dados que precisam ser manipulados e analisados em sequência.

5.1.2. Tuplas

Definição:
Tuplas são sequências ordenadas de itens, semelhantes às listas. No entanto, ao contrário das listas, as tuplas são imutáveis, ou seja, seus elementos não podem ser modificados após a criação.

Características: - Imutáveis: Uma vez criada, você não pode adicionar, remover ou alterar elementos de uma tupla. - Ordenadas: Os itens em uma tupla mantêm uma ordem específica. - Indexadas: Você pode acessar os itens em uma tupla usando índices (a posição do item na tupla, começando em 0). - Permitem duplicatas: Uma tupla pode conter múltiplos itens com o mesmo valor.

Sintaxe:
Tuplas são criadas usando parênteses ( ) e os itens são separados por vírgulas.

Exemplo de Código em Python:

# Exemplo de criação de uma tupla
minha_tupla = (1, 2, 3, 4, 5)

# Acessando elementos da tupla
print(minha_tupla[0])  # Saída: 1
print(minha_tupla[2])  # Saída: 3

# Tentando modificar um elemento da tupla (isso causará um erro)
try:
    minha_tupla[1] = 10  # Isso causará um TypeError
except TypeError as e:
    print(f"Erro: {e}")

# Iterando sobre uma tupla
for item in minha_tupla:
    print(item)

Resultado:

1
3
Erro: 'tuple' object does not support item assignment
1
2
3
4
5

Aplicação em Engenharia:
Tuplas são úteis para representar conjuntos de dados que não devem ser alterados, como coordenadas de um ponto, parâmetros fixos de um experimento ou registros imutáveis de configuração.

5.1.3. Dicionários

Definição:
Dicionários são coleções não ordenadas de pares chave-valor. Cada chave é única dentro do dicionário e é usada para acessar o valor correspondente.

Características: - Mutáveis: Você pode adicionar, remover ou alterar pares chave-valor em um dicionário. - Não ordenados: Os itens em um dicionário não têm uma ordem específica (em versões recentes do Python, a ordem de inserção é mantida, mas não deve ser usada como regra). - Acessados por chave: Você acessa os valores em um dicionário usando suas chaves, não índices. - Chaves únicas: Cada chave em um dicionário deve ser única.

Sintaxe:
Dicionários são criados usando chaves { }, com pares chave-valor separados por dois pontos : e os pares separados por vírgulas.

Exemplo de Código em Python:

# Exemplo de criação de um dicionário
meu_dicionario = {
    'nome': 'João',
    'idade': 30,
    'cidade': 'São Paulo'
}

# Acessando valores no dicionário
print(meu_dicionario['nome'])   # Saída: João
print(meu_dicionario['idade'])  # Saída: 30

# Modificando um valor no dicionário
meu_dicionario['idade'] = 31
print(meu_dicionario)  # Saída: {'nome': 'João', 'idade': 31, 'cidade': 'São Paulo'}

# Adicionando um novo par chave-valor
meu_dicionario['profissao'] = 'Engenheiro'
print(meu_dicionario)  # Saída: {'nome': 'João', 'idade': 31, 'cidade': 'São Paulo', 'profissao': 'Engenheiro'}

# Removendo um par chave-valor
del meu_dicionario['cidade']
print(meu_dicionario)  # Saída: {'nome': 'João', 'idade': 31, 'profissao': 'Engenheiro'}

# Iterando sobre um dicionário
for chave, valor in meu_dicionario.items():
    print(f"{chave}: {valor}")

Resultado:

João
30
{'nome': 'João', 'idade': 31, 'cidade': 'São Paulo'}
{'nome': 'João', 'idade': 31, 'cidade': 'São Paulo', 'profissao': 'Engenheiro'}
{'nome': 'João', 'idade': 31, 'profissao': 'Engenheiro'}
nome: João
idade: 31
profissao: Engenheiro

Aplicação em Engenharia:
Dicionários são ideais para armazenar dados associados a identificadores únicos, como medições de sensores (por exemplo, {‘sensor1’: 220.5, ‘sensor2’: 221.0}), propriedades de materiais, parâmetros de equipamentos ou resultados de experimentos, permitindo acesso rápido e organizado às informações.

5.1.4. Escolha da Estrutura de Dados

Ao desenvolver um programa, a escolha da estrutura de dados adequada é fundamental para garantir eficiência, clareza e facilidade de manutenção do código. Cada estrutura (lista, tupla ou dicionário) possui características próprias que a tornam mais indicada para determinadas situações.

Fatores a considerar ao escolher uma estrutura de dados:

1. Tipo de Dados:
   Que tipo de informação você precisa armazenar?
   • Listas: sequências de itens que podem mudar ao longo do tempo (ex: medições, resultados de experimentos).
   • Tuplas: conjuntos de dados fixos e imutáveis (ex: coordenadas, parâmetros constantes).
   • Dicionários: dados associados a identificadores únicos (ex: leituras de sensores, propriedades de materiais).
2. Operações Necessárias:
   Quais operações você precisa realizar com os dados?
   • Busca por posição (índice): listas e tuplas.
   • Busca por chave: dicionários.
   • Inserção, remoção ou alteração: listas e dicionários (tuplas não permitem).
3. Desempenho:
   Existem requisitos de desempenho específicos?
   • Dicionários oferecem acesso rápido por chave.
   • Listas são eficientes para operações sequenciais e ordenadas.
   • Tuplas são mais rápidas para leitura e ocupam menos memória quando imutabilidade é desejada.
4. Complexidade e Manutenção:
   Qual é a complexidade da implementação e manutenção?
   • Estruturas simples facilitam a leitura e manutenção do código.
   • Escolher a estrutura correta reduz a necessidade de adaptações futuras.

Resumo prático:

Exemplo de aplicação:

• Lista: Armazenar temperaturas medidas ao longo do tempo.
• Tupla: Representar as coordenadas (x, y, z) de um ponto.
• Dicionário: Relacionar o nome de cada sensor à sua leitura de tensão.

Escolher a estrutura de dados correta pode melhorar significativamente a eficiência, a clareza e a robustez do seu código em aplicações de engenharia.

5.1.5. Exercício Proposto: Análise de Dados de Sensores de Tensão em um Sistema de Distribuição de Energia

Descrição:
Um engenheiro eletricista precisa analisar dados de sensores de tensão instalados em diferentes pontos de um sistema de distribuição de energia. O programa deve armazenar os dados dos sensores, calcular estatísticas básicas (média, máximo, mínimo) e identificar possíveis anomalias (tensões fora de uma faixa aceitável).

Requisitos: 1. Armazenamento dos Dados dos Sensores: - Utilizar um dicionário para armazenar as informações de cada sensor. As chaves do dicionário serão os nomes dos sensores (strings) e os valores serão listas contendo as leituras de tensão (floats) ao longo de um período. - Utilizar uma tupla para representar a faixa de tensão aceitável (tensão mínima e tensão máxima). 2. Cálculo de Estatísticas: - Criar funções para calcular a média, o valor máximo e o valor mínimo de uma lista de tensões. 3. Identificação de Anomalias: - Criar uma função para verificar se alguma leitura de tensão em uma lista está fora da faixa aceitável definida pela tupla. 4. Saída de Dados: - Exibir os dados dos sensores, as estatísticas calculadas e as informações sobre possíveis anomalias.

Código do Programa:

# Análise de Dados de Sensores de Tensão

def calcular_media(tensoes):
    """Calcula a média de uma lista de tensões."""
    return sum(tensoes) / len(tensoes)

def calcular_maximo(tensoes):
    """Calcula o valor máximo de uma lista de tensões."""
    return max(tensoes)

def calcular_minimo(tensoes):
    """Calcula o valor mínimo de uma lista de tensões."""
    return min(tensoes)

def verificar_anomalias(tensoes, faixa_aceitavel):
    """Verifica se há tensões fora da faixa aceitável.
    Args:
        tensoes (list): Lista de leituras de tensão.
        faixa_aceitavel (tuple): Tupla contendo a tensão mínima e máxima aceitáveis.
    Returns:
        list: Lista de índices das tensões fora da faixa.
    """
    anomalias = []
    for i, tensao in enumerate(tensoes):
        if tensao < faixa_aceitavel[0] or tensao > faixa_aceitavel[1]:
            anomalias.append(i)
    return anomalias

# 1. Armazenamento dos Dados dos Sensores
dados_sensores = {
    "Sensor_A": [120.5, 121.0, 118.9, 122.1, 115.5],
    "Sensor_B": [220.2, 219.8, 221.1, 218.5, 225.0],
    "Sensor_C": [135.7, 136.0, 134.9, 137.2, 133.3]
}

# Tupla: Faixa de Tensão Aceitável (mínimo, máximo)
faixa_tensao_aceitavel = (117.0, 222.0)

# 2. Cálculo de Estatísticas e 3. Identificação de Anomalias
print("Análise de Dados de Sensores de Tensão\n")

for sensor, tensoes in dados_sensores.items():
    print(f"--- Sensor: {sensor} ---")
    media = calcular_media(tensoes)
    maximo = calcular_maximo(tensoes)
    minimo = calcular_minimo(tensoes)
    print(f"Média: {media:.2f} V")
    print(f"Máximo: {maximo:.2f} V")
    print(f"Mínimo: {minimo:.2f} V")

    anomalias = verificar_anomalias(tensoes, faixa_tensao_aceitavel)
    if anomalias:
        print(f"ALERTA: Anomalias detectadas nas leituras: {anomalias}")
    else:
        print("Nenhuma anomalia detectada.")
    print()

Saída Esperada:

Análise de Dados de Sensores de Tensão

--- Sensor: Sensor_A ---
Média: 119.60 V
Máximo: 122.10 V
Mínimo: 115.50 V
ALERTA: Anomalias detectadas nas leituras: [3, 4]

--- Sensor: Sensor_B ---
Média: 220.92 V
Máximo: 225.00 V
Mínimo: 218.50 V
ALERTA: Anomalias detectadas nas leituras: [4]

--- Sensor: Sensor_C ---
Média: 135.42 V
Máximo: 137.20 V
Mínimo: 133.30 V
Nenhuma anomalia detectada.

Explicação dos Conceitos Utilizados:

• Dicionários:
  Usados para armazenar os dados de todos os sensores, permitindo acesso rápido às leituras de cada sensor por nome.
• Listas:
  Armazenam as leituras de tensão de cada sensor, facilitando operações como cálculo de média, máximo e mínimo.
• Tuplas:
  Utilizadas para definir a faixa de tensão aceitável, pois são valores fixos que não devem ser alterados durante a execução do programa.
• Funções:
  Funções específicas para calcular estatísticas e identificar anomalias tornam o código modular, reutilizável e fácil de manter.

Aplicação em Engenharia:
Este exercício demonstra como listas, tuplas e dicionários podem ser usados em conjunto para organizar, analisar e monitorar dados de sensores em sistemas de engenharia elétrica, permitindo a identificação rápida de anomalias e a tomada de decisões baseada em dados.

5.1.6. Destaque dos Conceitos

Neste exercício, utilizamos de forma integrada as três principais estruturas de dados do Python: dicionários, listas e tuplas. Veja como cada uma delas foi aplicada:

Dicionários

• O dicionário dados_sensores é usado para armazenar os dados de todos os sensores.
• As chaves do dicionário (strings como "Sensor_A", "Sensor_B") representam os nomes dos sensores, permitindo acessar facilmente os dados de um sensor específico.
• Os valores do dicionário são listas, o que permite armazenar múltiplas leituras de tensão para cada sensor.
• O loop for sensor, tensoes in dados_sensores.items(): demonstra como iterar sobre os itens de um dicionário (chave e valor).

Listas

• As leituras de tensão de cada sensor são armazenadas em uma lista (por exemplo, [120.5, 121.0, 118.9, 122.1, 115.5]).
• As listas permitem armazenar uma sequência de valores (as tensões ao longo do tempo) para cada sensor.
• As funções calcular_media(), calcular_maximo() e calcular_minimo() recebem uma lista como argumento e operam sobre ela.
• A função verificar_anomalias() retorna uma lista contendo os índices das leituras anômalas.
• O acesso a elementos específicos da lista é feito por índice (por exemplo, tensoes[0] para acessar a primeira leitura).

Tuplas

• A tupla faixa_tensao_aceitavel é usada para armazenar a faixa de tensão aceitável (tensão mínima e máxima).
• A tupla é utilizada porque a faixa de tensão geralmente é um valor fixo que não deve ser alterado durante a execução do programa.
• A função verificar_anomalias() recebe a tupla como argumento para comparar as leituras de tensão com os limites.
• O acesso aos elementos da tupla é feito por índice (por exemplo, faixa_aceitavel[0] para acessar a tensão mínima).

Resumo:
Este exercício demonstra como dicionários, listas e tuplas podem ser usados em conjunto para resolver um problema prático de engenharia elétrica, organizando, armazenando e manipulando dados de sensores de forma eficiente e estruturada.

5.2. Iteração e Manipulação de Dados

Uma vez que entendemos as estruturas de dados básicas (listas, tuplas e dicionários), é crucial aprender como percorrer (iterar) seus elementos e realizar diversas operações de manipulação. Esta seção aborda as técnicas e métodos mais comuns para trabalhar com esses dados em Python.

5.2.1. Iteração em Listas, Tuplas e Dicionários

Iteração é o processo de percorrer cada item em uma estrutura de dados (como uma lista, tupla ou dicionário) para acessar ou processá-lo. Python fornece maneiras eficientes de realizar essa tarefa, principalmente usando os loops for e while.

Iterando com o loop for

O loop for é a forma mais comum e elegante de iterar em Python.

• Listas e Tuplas: ```python # Exemplo de iteração em uma lista minha_lista = [1, 2, 3, 4, 5] for item in minha_lista: print(item)

  # Exemplo de iteração em uma tupla minha_tupla = (10, 20, 30, 40, 50) for item in minha_tupla: print(item) **Resultado:**plaintext 1 2 3 4 5 10 20 30 40 50 ```

• Dicionários: python # Exemplo de iteração em um dicionário meu_dicionario = {'a': 1, 'b': 2, 'c': 3} for chave, valor in meu_dicionario.items(): print(f"{chave}: {valor}") Resultado: plaintext a: 1 b: 2 c: 3

Iterando com o loop while

O loop while é menos comum para iteração direta em estruturas de dados, mas é útil quando você precisa de mais controle sobre a condição de parada.

• Listas e Tuplas: python # Exemplo de iteração em uma lista com WHILE minha_lista = [1, 2, 3, 4, 5] i = 0 while i < len(minha_lista): print(minha_lista[i]) i += 1 Resultado: plaintext 1 2 3 4 5

• Dicionários:
  Iterar em dicionários com while é raro e geralmente não recomendado, pois dicionários não são indexados por posição. Se necessário, converta as chaves em uma lista: python meu_dicionario = {'a': 1, 'b': 2, 'c': 3} chaves = list(meu_dicionario.keys()) i = 0 while i < len(chaves): chave = chaves[i] valor = meu_dicionario[chave] print(f"{chave}: {valor}") i += 1 Resultado: plaintext a: 1 b: 2 c: 3

List Comprehensions

Python oferece uma forma concisa de criar listas usando compreensão de lista. Isso é eficiente e legível para certas operações.

# Exemplo de list comprehension
quadrados = [x**2 for x in range(1, 6)]
print(quadrados)  # Saída: [1, 4, 9, 16, 25]

Resultado:

[1, 4, 9, 16, 25]

Generator Expressions

Semelhantes às list comprehensions, mas criam um gerador (iterador) em vez de uma lista. São mais eficientes em termos de memória para grandes conjuntos de dados.

# Exemplo de generator expression
gerador = (x**2 for x in range(1, 6))
for quadrado in gerador:
    print(quadrado)

Resultado:

1
4
9
16
25

Dicas para Escolha do Método

• Use for para iteração simples e direta em listas, tuplas e dicionários.
• Use enumerate() se precisar do índice durante a iteração.
• Use while quando precisar de controle mais fino sobre a condição de parada, mas evite para iteração simples.
• Use list comprehensions para criar listas de forma concisa e eficiente.
• Use generator expressions para economizar memória ao iterar sobre grandes conjuntos de dados.

Resumo:
Dominar as técnicas de iteração é fundamental para trabalhar efetivamente com estruturas de dados em Python, permitindo que você processe e analise dados de maneira eficiente em aplicações de engenharia.

5.2.2. Exercício Proposto: Análise de Dados de Teste de Tração

Descrição:
Um engenheiro mecânico realizou um teste de tração em um novo tipo de aço. O teste gerou uma série de dados de força (em Newtons) e alongamento (em milímetros). O objetivo é usar Python para analisar esses dados, calcular a tensão e a deformação, e determinar propriedades importantes do material, como o módulo de elasticidade e a tensão de escoamento.

Requisitos: 1. Armazenamento dos Dados: - Armazenar os dados de força e alongamento em listas. 2. Cálculo de Tensão e Deformação: - Criar funções para calcular a tensão (σ) e a deformação (ε) para cada ponto de dado. - Tensão (σ) = Força / Área da seção transversal inicial - Deformação (ε) = Alongamento / Comprimento inicial 3. Determinação do Módulo de Elasticidade: - Calcular o módulo de elasticidade (E) a partir da inclinação da parte linear inicial da curva tensão-deformação. 4. Determinação da Tensão de Escoamento: - Estimar a tensão de escoamento (σy) usando o método do deslocamento de 0,2%. 5. Saída de Dados: - Exibir a curva tensão-deformação (em texto) e as propriedades do material calculadas.

Código Python de Exemplo:

# Análise de Dados de Teste de Tração

def calcular_tensao(forcas, area_inicial):
    """Calcula a tensão a partir da força e da área inicial."""
    return [forca / area_inicial for forca in forcas]

def calcular_deformacao(alongamentos, comprimento_inicial):
    """Calcula a deformação a partir do alongamento e do comprimento inicial."""
    return [alongamento / comprimento_inicial for alongamento in alongamentos]

def calcular_modulo_elasticidade(deformacoes, tensoes, num_pontos=10):
    """
    Estima o módulo de elasticidade a partir da inclinação inicial da curva tensão-deformação.
    Usa os primeiros 'num_pontos' para ajustar uma linha.
    """
    if len(deformacoes) < num_pontos:
        num_pontos = len(deformacoes)
    soma_xy = sum(deformacoes[i] * tensoes[i] for i in range(num_pontos))
    soma_x = sum(deformacoes[i] for i in range(num_pontos))
    soma_y = sum(tensoes[i] for i in range(num_pontos))
    soma_x2 = sum(deformacoes[i]**2 for i in range(num_pontos))
    n = num_pontos
    numerador = n * soma_xy - soma_x * soma_y
    denominador = n * soma_x2 - soma_x**2
    if denominador == 0:
        return 0
    else:
        return numerador / denominador

def estimar_tensao_escoamento(deformacoes, tensoes, offset=0.002):
    """
    Estima a tensão de escoamento usando o método do deslocamento de 0,2%.
    """
    for i in range(len(deformacoes)):
        if deformacoes[i] >= offset:
            if i > 0:
                deformacao_anterior = deformacoes[i-1]
                tensao_anterior = tensoes[i-1]
                inclinacao = (tensoes[i] - tensao_anterior) / (deformacoes[i] - deformacao_anterior)
                tensao_escoamento = tensao_anterior + inclinacao * (offset - deformacao_anterior)
                return tensao_escoamento
            else:
                return tensoes[0]
    return None

# 1. Dados de Entrada
forcas = [0, 1000, 2500, 4000, 5500, 7000, 8500, 9000, 8800, 8500]  # Forças em N
alongamentos = [0, 0.2, 0.5, 0.8, 1.1, 1.4, 1.7, 2.0, 2.5, 3.0]  # Alongamentos em mm
area_inicial = 50  # Área da seção transversal inicial em mm²
comprimento_inicial = 50  # Comprimento inicial em mm

# 2. Calcular Tensão e Deformação
tensoes = calcular_tensao(forcas, area_inicial)
deformacoes = calcular_deformacao(alongamentos, comprimento_inicial)

# 3. Determinar o Módulo de Elasticidade
modulo_elasticidade = calcular_modulo_elasticidade(deformacoes, tensoes)

# 4. Determinar a Tensão de Escoamento
tensao_escoamento = estimar_tensao_escoamento(deformacoes, tensoes)

# 5. Saída de Dados
print("Análise de Dados de Teste de Tração\n")
print("Curva Tensão-Deformação:")
for i in range(len(tensoes)):
    print(f"Tensão: {tensoes[i]:.2f} MPa, Deformação: {deformacoes[i]:.4f}")

print(f"\nMódulo de Elasticidade: {modulo_elasticidade:.2f} MPa")
print(f"Tensão de Escoamento (0.2%): {tensao_escoamento:.2f} MPa")

Saída Esperada:

Análise de Dados de Teste de Tração
Curva Tensão-Deformação:
Tensão: 0.00 MPa, Deformação: 0.0000
Tensão: 20.00 MPa, Deformação: 0.0040
Tensão: 50.00 MPa, Deformação: 0.0100
Tensão: 80.00 MPa, Deformação: 0.0160
Tensão: 110.00 MPa, Deformação: 0.0220
Tensão: 140.00 MPa, Deformação: 0.0280
Tensão: 170.00 MPa, Deformação: 0.0340
Tensão: 180.00 MPa, Deformação: 0.0400
Tensão: 176.00 MPa, Deformação: 0.0500
Tensão: 170.00 MPa, Deformação: 0.0600

Módulo de Elasticidade: 5000.00 MPa
Tensão de Escoamento (0.2%): 25.00 MPa

Explicação dos Conceitos Utilizados:

• Listas:
  Utilizadas para armazenar os dados de força e alongamento, permitindo fácil acesso e manipulação dos dados.
• Funções:
  Criadas para calcular a tensão, deformação, módulo de elasticidade e tensão de escoamento, promovendo modularidade e reutilização do código.
• List Comprehensions:
  Utilizadas para calcular tensões e deformações de forma concisa e eficiente.
• Iteração:
  Utilizada para percorrer os dados de entrada e calcular os resultados desejados, permitindo a aplicação de operações em cada elemento das listas.
• Cálculos Matemáticos:
  Realizados para determinar a tensão, deformação, módulo de elasticidade e tensão de escoamento, utilizando fórmulas e métodos apropriados.
• Controle de Fluxo:
  Utilizado para verificar condições e calcular a tensão de escoamento com base no deslocamento de 0,2%, garantindo que o programa funcione corretamente mesmo com diferentes conjuntos de dados.

Aplicação em Engenharia:
Este exercício mostra como Python pode ser utilizado para analisar dados experimentais de materiais, calcular propriedades mecânicas e apoiar a tomada de decisão em projetos de engenharia mecânica.

5.3. Aplicações em Vetores de Parâmetros de Processo

Em muitas áreas da engenharia, os processos são caracterizados por múltiplos parâmetros que influenciam seu comportamento e desempenho. Esses parâmetros podem incluir temperaturas, pressões, vazões, velocidades, concentrações, entre outros. Para organizar e manipular esses conjuntos de dados, é comum representá-los como vetores. As estruturas de dados de Python (listas, tuplas e dicionários) são ferramentas poderosas para trabalhar com esses vetores de parâmetros de processo.

5.3.1. Representação de Vetores de Parâmetros

Em engenharia, é comum lidar com conjuntos de parâmetros que representam o estado ou as condições de um processo, como temperaturas, pressões, vazões, concentrações, entre outros. Esses conjuntos podem ser organizados em vetores de parâmetros, e a escolha da estrutura de dados adequada em Python facilita a manipulação e análise dessas informações.

Principais estruturas para representar vetores de parâmetros:

• Listas:
  São adequadas quando a ordem dos parâmetros é importante e os valores podem mudar ao longo do tempo.
  Exemplo:

  temperaturas = [350.0, 355.2, 360.1, 358.7]  # Temperaturas medidas em um reator químico a cada segundo

• Tuplas:
  São úteis quando a ordem dos parâmetros é importante e os valores são fixos (imutáveis).
  Exemplo:

  coordenadas = (10.0, 5.5, 3.2)  # Coordenadas (x, y, z) de um ponto em um sistema de controle de robô

• Dicionários:
  São ideais quando você precisa associar um nome (chave) a cada parâmetro, facilitando o acesso direto pelo identificador.
  Exemplo:

  parametros_caldeira = {
      "temperatura": 500,         # em °C
      "pressao": 10,              # em bar
      "vazao_combustivel": 2.5    # em m³/h
  }

Resumo prático:

Aplicação em Engenharia:
A escolha correta da estrutura de dados permite organizar, acessar e manipular eficientemente os parâmetros de processo, facilitando análises, simulações e tomadas de decisão em projetos de engenharia.

5.3.2. Exercício Proposto: Análise do Desempenho de um Reator Químico Batch

Descrição:
Um engenheiro químico está analisando o desempenho de um reator químico batch onde ocorre uma reação de primeira ordem. O objetivo é usar Python para armazenar e manipular dados experimentais do reator (temperatura, concentração do reagente ao longo do tempo), calcular a constante de velocidade da reação (k) e gerar gráficos para visualizar a evolução da concentração e da temperatura com o tempo.

Requisitos: 1. Armazenar Dados Experimentais: - Utilizar listas para armazenar: - Tempo (minutos) - Concentrações do reagente (mol/L) - Temperaturas do reator (°C) 2. Calcular a Constante de Velocidade (k): - Aplicar a equação de reação de primeira ordem (linearizada):
ln(C(t)) = ln(C0) - k*t - Realizar regressão linear nos dados ln(C(t)) vs. t para determinar k (negativo da inclinação da reta). 3. Gerar Gráficos (Texto): - Criar funções para gerar representações textuais dos gráficos: - Gráfico de Concentração vs. Tempo - Gráfico de Temperatura vs. Tempo 4. Saída de Dados: - Exibir: - Constante de velocidade (k) - Representações textuais dos gráficos

5.3.3. Conceitos Aplicados no Código

Neste exercício, diversos conceitos fundamentais de programação e engenharia foram aplicados para analisar o desempenho de um reator químico batch. Veja os principais pontos:

1. Vetores como Parâmetros de Processo
   • As listas tempos, concentracoes e temperaturas representam vetores de parâmetros de processo, comuns em engenharia para modelar a evolução de variáveis ao longo do tempo.
   • Essa abordagem permite analisar tendências, identificar padrões e realizar cálculos sobre conjuntos de dados experimentais.
2. Reação de Primeira Ordem

   • A função calcular_constante_velocidade utiliza regressão linear sobre o logaritmo das concentrações, assumindo cinética de primeira ordem:

     ln(C(t)) = ln(C0) - k * t

   • O valor de k (constante de velocidade) é extraído da inclinação da reta ajustada aos dados experimentais, permitindo avaliar a eficiência e a velocidade da reação.

3. Representação Gráfica (via Texto)
   • A função gerar_grafico_texto converte os vetores de dados em gráficos ASCII, possibilitando uma visualização simples da evolução das variáveis mesmo sem bibliotecas gráficas.
   • Essa técnica é útil para ambientes restritos ou para documentação rápida dos resultados.
4. Correlação entre Variáveis
   • Os dados organizados em listas permitem analisar como diferentes variáveis se relacionam, por exemplo:
     • Como a temperatura influencia a constante de velocidade (k)
     • Como a concentração varia com o tempo e a temperatura
   • Embora o código não calcule diretamente correlações estatísticas, a estrutura facilita esse tipo de análise.
5. Modularidade e Reutilização
   • O uso de funções específicas para cada tarefa (cálculo de constante, geração de gráfico, etc.) torna o código modular, reutilizável e fácil de manter.
   • Essa prática é essencial para projetos maiores e para a colaboração entre engenheiros.

Resumo:
O exercício integra conceitos de vetores de parâmetros, análise cinética, visualização de dados e modularização de código, mostrando como Python pode ser uma ferramenta poderosa para a análise e otimização de processos em engenharia química.

5.3.4. Exercício Proposto: Resolução

Neste item, apresentamos a resolução detalhada do exercício de análise do desempenho de um reator químico batch, integrando os conceitos de vetores de parâmetros, funções e manipulação de dados em Python.

O objetivo é mostrar, passo a passo, como implementar um programa que armazena dados experimentais (tempo, concentração e temperatura), calcula a constante de velocidade da reação por regressão linear, e gera representações gráficas textuais para facilitar a visualização dos resultados.

A resolução inclui:

• Definição de funções para calcular a constante de velocidade da reação (k) e para gerar gráficos em formato texto (ASCII), promovendo modularidade e reutilização do código.
• Organização dos dados experimentais em listas, representando os vetores de parâmetros típicos de processos químicos.
• Aplicação de técnicas matemáticas (como regressão linear) para extrair informações relevantes dos dados, como a constante de velocidade.
• Visualização dos resultados por meio de gráficos textuais, permitindo interpretar rapidamente o comportamento do sistema mesmo sem bibliotecas gráficas.
• Saída estruturada, exibindo a constante de velocidade calculada e os gráficos de concentração e temperatura ao longo do tempo.

Este exercício reforça a importância de combinar estruturas de dados, funções e lógica de programação para resolver problemas reais de engenharia, tornando o código mais organizado, eficiente e fácil de manter. A abordagem apresentada pode ser adaptada para outros tipos de análises experimentais e processos industriais, evidenciando a versatilidade do Python na engenharia.

Código Python de Exemplo:

import math

def calcular_constante_velocidade(tempos, concentracoes):
    """
    Calcula a constante de velocidade de uma reação de primeira ordem usando regressão linear.
    """
    ln_concentracoes = [math.log(c) for c in concentracoes]
    n = len(tempos)
    soma_t = sum(tempos)
    soma_lnc = sum(ln_concentracoes)
    soma_t_lnc = sum(tempos[i] * ln_concentracoes[i] for i in range(n))
    soma_t2 = sum(t**2 for t in tempos)

    numerador = n * soma_t_lnc - soma_t * soma_lnc
    denominador = n * soma_t2 - soma_t**2

    if denominador == 0:
        return 0
    inclinacao = numerador / denominador
    k = -inclinacao
    return k

def gerar_grafico_texto(x_dados, y_dados, x_label, y_label):
    """
    Gera uma representação textual aproximada de um gráfico.
    """
    min_x = min(x_dados)
    max_x = max(x_dados)
    min_y = min(y_dados)
    max_y = max(y_dados)

    largura = 50
    altura = 20

    x_intervalo = (max_x - min_x) / largura if max_x != min_x else 1
    y_intervalo = (max_y - min_y) / altura if max_y != min_y else 1

    matriz_grafico = [[' ' for _ in range(largura + 1)] for _ in range(altura + 1)]

    # Marcar os pontos
    for i in range(len(x_dados)):
        x_pos = int((x_dados[i] - min_x) / x_intervalo)
        y_pos = altura - int((y_dados[i] - min_y) / y_intervalo)
        if 0 <= x_pos <= largura and 0 <= y_pos <= altura:
            matriz_grafico[y_pos][x_pos] = '*'

    # Eixos
    for i in range(altura + 1):
        matriz_grafico[i][0] = '|'
    for j in range(largura + 1):
        matriz_grafico[altura][j] = '-'

    # Rótulos (simplificado)
    matriz_grafico[0][largura] = y_label[0]  # Primeira letra do rótulo y
    matriz_grafico[altura][largura] = x_label[0]  # Primeira letra do rótulo x

    grafico_texto = "\n".join(["".join(linha) for linha in matriz_grafico])
    return grafico_texto

# 1. Dados Experimentais
tempos = [0, 5, 10, 15, 20, 25, 30]  # minutos
concentracoes = [1.6, 1.2, 0.9, 0.6, 0.45, 0.34, 0.25]  # mol/L
temperaturas = [50.0, 52.5, 54.8, 57.1, 59.2, 61.1, 62.8]  # °C

# 2. Calcular a Constante de Velocidade
k = calcular_constante_velocidade(tempos, concentracoes)

# 3. Gerar Gráficos (Texto)
grafico_concentracao = gerar_grafico_texto(tempos, concentracoes, "Tempo (min)", "Concentração (mol/L)")
grafico_temperatura = gerar_grafico_texto(tempos, temperaturas, "Tempo (min)", "Temperatura (°C)")

# 4. Saída de Dados
print("Análise de Reator Químico Batch\n")
print(f"Constante de Velocidade (k): {k:.4f} min^-1\n")

print("Gráfico: Concentração vs. Tempo\n")
print(grafico_concentracao)

print("\nGráfico: Temperatura vs. Tempo\n")
print(grafico_temperatura)

Saída Esperada:

Explicação dos Conceitos Utilizados:

• Listas:
  Utilizadas para armazenar os dados de tempo, concentração e temperatura.
• Funções:
  Criadas para calcular a constante de velocidade e gerar gráficos textuais, promovendo modularidade.
• List Comprehensions:
  Usadas para calcular o logaritmo natural das concentrações de forma concisa.
• Iteração:
  Utilizada para percorrer os dados e construir os gráficos.
• Cálculos Matemáticos:
  Realizados para determinar a constante de velocidade da reação.
• Controle de Fluxo:
  Utilizado para evitar divisão por zero e garantir robustez no código.

Aplicação em Engenharia:
Este exercício demonstra como Python pode ser utilizado para analisar dados experimentais de reatores químicos, calcular propriedades cinéticas e gerar visualizações textuais dos resultados. A manipulação eficiente de vetores de parâmetros de processo é essencial para otimizar o desempenho e a segurança em processos químicos industriais.

5.4. Conclusão

Neste módulo, exploramos as principais estruturas de dados do Python — listas, tuplas e dicionários — e aprendemos como utilizá-las para organizar, armazenar e manipular informações de forma eficiente em aplicações de engenharia. Vimos que:

• Listas são ideais para coleções mutáveis e ordenadas de dados, permitindo fácil acesso, modificação e iteração sobre elementos.
• Tuplas são úteis para agrupar dados imutáveis, garantindo integridade e segurança em situações onde os valores não devem ser alterados.
• Dicionários oferecem acesso rápido a informações associadas a identificadores únicos, sendo essenciais para organizar dados complexos e heterogêneos.

Também praticamos técnicas de iteração, manipulação e análise de dados, além de resolver exercícios aplicados à engenharia, como análise de sensores, testes de tração e desempenho de reatores. Essas atividades demonstraram como as estruturas de dados podem ser combinadas para solucionar problemas reais, tornando o código mais organizado, legível e eficiente.

O domínio dessas ferramentas é fundamental para qualquer engenheiro ou cientista que deseje automatizar tarefas, analisar grandes volumes de dados e desenvolver soluções computacionais robustas. Ao aplicar corretamente listas, tuplas e dicionários, você estará preparado para enfrentar desafios cada vez mais complexos na programação Python voltada à engenharia.

6. Manipulação de Arquivos e Dados

A capacidade de interagir com arquivos e analisar dados é essencial para o trabalho de engenheiros e cientistas. Nesta seção, vamos explorar as técnicas e ferramentas fundamentais para a manipulação de dados em Python, focando inicialmente na leitura e escrita de arquivos nos formatos .txt e .csv, que servem como base para armazenar e trocar informações, prosseguindo com uma introdução à biblioteca PANDAS, uma biblioteca que oferece estruturas de dados e funções otimizadas para análise de dados, simplificando tarefas como limpeza, organização e transformação, e, por fim, aplicando esses conhecimentos na análise de dados experimentais, provenientes de medições reais, e de simulações computacionais, demonstrando como extrair informações significativas e validar modelos.

6.1. Leitura e Escrita de Arquivos .txt e .csv

A manipulação de arquivos é fundamental para armazenar, recuperar e compartilhar dados em projetos de engenharia. Python oferece recursos simples e poderosos para trabalhar com arquivos de texto (.txt) e arquivos CSV (.csv), que são amplamente utilizados para registrar medições, resultados de simulações e tabelas de dados.

6.1.1. Conceitos

• Arquivos de texto (.txt):
  São arquivos simples, compostos por linhas de texto. Podem ser usados para registrar listas de valores, relatórios ou logs de experimentos.
  Operações comuns: abrir, ler (readline, readlines, read), escrever (write, writelines), fechar.

• Arquivos CSV (.csv):
  São arquivos de texto com dados organizados em formato tabular, onde cada linha representa um registro e os valores são separados por vírgulas (ou outro delimitador). Muito usados para exportar/importar dados entre softwares (Excel, bancos de dados, etc.).
  Em Python, o módulo csv facilita a leitura e escrita desses arquivos.

• Modos de abertura de arquivo:

  • 'r': leitura
    
  • 'w': escrita (sobrescreve o arquivo)
    
  • 'a': escrita (adiciona ao final do arquivo)
    
  • 'r+': leitura e escrita

• Tratamento de erros:
  O uso de blocos try-except-finally é recomendado para evitar falhas ao manipular arquivos inexistentes ou corrompidos.

6.1.2. Exemplos

1. Ler um arquivo .txt com dados de temperatura e extrair a média

Arquivo de texto temperaturas.txt:

25.0
26.5
24.8
27.2
25.5

Código Python de Exemplo:

# Leitura de arquivo .txt e cálculo da média
def calcular_media_temperaturas(arquivo):
    try:
        with open(arquivo, 'r') as file:
            temperaturas = [float(linha.strip()) for linha in file.readlines()]
            media = sum(temperaturas) / len(temperaturas)
            return media
    except FileNotFoundError:
        print(f"Erro: O arquivo {arquivo} não foi encontrado.")
        return None
    except Exception as e:
        print(f"Erro ao ler o arquivo: {e}")
        return None

# Uso da função
media_temperatura = calcular_media_temperaturas('temperaturas.txt')
if media_temperatura is not None:
    print(f"Média de Temperaturas: {media_temperatura:.2f} °C")

Saída Esperada:

Média de Temperaturas: 25.50 °C

2. Escrever uma lista de resultados de simulação em um arquivo .txt

Código Python de Exemplo:

def escrever_resultados_simulacao(arquivo, resultados):
    try:
        with open(arquivo, 'w') as file:
            for resultado in resultados:
                file.write(f"{resultado}\n")
    except Exception as e:
        print(f"Erro ao escrever no arquivo: {e}")

# Uso da função
resultados = [25.5, 26.0, 24.8, 27.2, 25.5]
escrever_resultados_simulacao('resultados.txt', resultados)

Saída Esperada:

Arquivo `resultados.txt` criado com os valores:

3. Ler e escrever arquivos CSV com o módulo csv

Código Python de Exemplo:

import csv

# Leitura de um arquivo CSV
with open('dados.csv', 'r', newline='') as csvfile:
    leitor = csv.reader(csvfile)
    for linha in leitor:
        print(linha)

# Escrita em um arquivo CSV
dados = [
    ['Tempo (s)', 'Temperatura (°C)'],
    [0, 25.0],
    [10, 26.5],
    [20, 27.2]
]
with open('resultados.csv', 'w', newline='') as csvfile:
    escritor = csv.writer(csvfile)
    escritor.writerows(dados)

Saída Esperada:

['Tempo (s)', 'Temperatura (°C)']
['0', '25.0']
['10', '26.5']
['20', '27.2']

Resumo:
A leitura e escrita de arquivos .txt e .csv são tarefas essenciais para registrar, analisar e compartilhar dados em projetos de engenharia. Dominar essas operações permite automatizar rotinas, integrar sistemas e documentar resultados de forma eficiente.

6.1.3. Exercício Proposto: Análise de Dados de Vazão em ETE

Descrição:
Em uma Estação de Tratamento de Esgoto (ETE), o controle preciso da vazão de água tratada é essencial para garantir a eficiência do processo e o cumprimento das normas ambientais. Um sistema de controle registra a vazão volumétrica da água limpa (efluente) em intervalos regulares. Os dados são armazenados em um arquivo CSV, onde cada linha contém o timestamp e o valor da vazão.

Objetivo:
Desenvolver um script Python para ler o arquivo CSV, analisar os dados de vazão e fornecer informações relevantes sobre o desempenho do sistema de controle.

Dados de Entrada:
Um arquivo CSV chamado vazao_efluente.csv com as seguintes colunas:
- Timestamp (formato: “AAAA-MM-DD HH:MM:SS”)
- Vazao_m3h (vazão volumétrica em metros cúbicos por hora)

Exemplo de conteúdo de vazao_efluente.csv:

Timestamp,Vazao_m3h
2023-01-01 00:00:00,100
2023-01-01 01:00:00,150
2023-01-01 02:00:00,200
2023-01-01 03:00:00,180
2023-01-01 04:00:00,220
2023-01-01 05:00:00,250

Tarefas:

1. Leitura do Arquivo CSV:
   • Desenvolver uma função ler_dados_vazao(nome_arquivo) que leia o arquivo CSV e retorne os dados em uma lista de tuplas, onde cada tupla contenha (timestamp, vazão).
   • Converter a coluna Timestamp para o tipo datetime usando o módulo datetime do Python.
   • Tratar possíveis erros de leitura de arquivo (FileNotFoundError) e conversão de dados (ValueError).
2. Análise dos Dados:
   • Desenvolver funções para calcular:
     • vazao_media(dados): Calcula a vazão média no período.
     • vazao_maxima(dados): Encontra a vazão máxima e o timestamp em que ocorreu.
     • vazao_minima(dados): Encontra a vazão mínima e o timestamp em que ocorreu.
3. Relatório:
   • Gerar um relatório que exiba:
     • A vazão média.
     • A vazão máxima e o timestamp em que ocorreu.
     • A vazão mínima e o timestamp em que ocorreu.
4. Escrita do Relatório:

   • Escrever o relatório em um arquivo de texto chamado relatorio_vazao.txt no seguinte formato:

     Relatório de Vazão do Efluente
     Data: AAAA-MM-DD
     Vazão Média: X m³/h
     Vazão Máxima: Y m³/h (Timestamp: AAAA-MM-DD HH:MM:SS)
     Vazão Mínima: Z m³/h (Timestamp: AAAA-MM-DD HH:MM:SS)

Código Python de Exemplo:

import csv
from datetime import datetime

def ler_dados_vazao(nome_arquivo):
    dados = []
    try:
        with open(nome_arquivo, 'r', newline='') as csvfile:
            leitor = csv.DictReader(csvfile)
            for linha in leitor:
                try:
                    timestamp = datetime.strptime(linha['Timestamp'], "%Y-%m-%d %H:%M:%S")
                    vazao = float(linha['Vazao_m3h'])
                    dados.append((timestamp, vazao))
                except ValueError as e:
                    print(f"Erro de conversão em linha: {linha} - {e}")
    except FileNotFoundError:
        print(f"Arquivo {nome_arquivo} não encontrado.")
    return dados

def vazao_media(dados):
    if not dados:
        return 0
    return sum(v for _, v in dados) / len(dados)

def vazao_maxima(dados):
    if not dados:
        return None, None
    return max(dados, key=lambda x: x[1])

def vazao_minima(dados):
    if not dados:
        return None, None
    return min(dados, key=lambda x: x[1])

def escrever_relatorio(nome_arquivo, data, media, maximo, minimo):
    with open(nome_arquivo, 'w') as f:
        f.write("Relatório de Vazão do Efluente\n")
        f.write(f"Data: {data}\n")
        f.write(f"Vazão Média: {media:.2f} m³/h\n")
        f.write(f"Vazão Máxima: {maximo[1]:.2f} m³/h (Timestamp: {maximo[0]})\n")
        f.write(f"Vazão Mínima: {minimo[1]:.2f} m³/h (Timestamp: {minimo[0]})\n")

# Uso das funções
dados = ler_dados_vazao('vazao_efluente.csv')
if dados:
    data_relatorio = dados[0][0].date()
    media = vazao_media(dados)
    maximo = vazao_maxima(dados)
    minimo = vazao_minima(dados)
    escrever_relatorio('relatorio_vazao.txt', data_relatorio, media, maximo, minimo)
    print("Relatório gerado com sucesso!")
else:
    print("Nenhum dado disponível para análise.")

Resumo:

Este exercício integra leitura de arquivos CSV, manipulação de datas, análise estatística simples e geração de relatórios automatizados, mostrando como Python pode ser aplicado para monitorar e documentar o desempenho de sistemas de engenharia ambiental.

6.1.4. Considerações Adicionais:

• Validação de Dados: É importante validar os dados lidos do arquivo para garantir que estão no formato esperado e evitar erros durante o processamento.
• Tratamento de Erros: Sempre trate possíveis erros ao ler ou escrever arquivos, como arquivos inexistentes ou problemas de permissão.
• Extensões Futuras:
  • Visualização: Como um passo adicional, você pode expandir este exercício para incluir a visualização dos dados de vazão usando bibliotecas como MAT_PLOT_LIB ou SEABORN. Isso permitiria uma análise mais intuitiva das tendências e padrões na vazão.
  • Análise Estatística: Para uma análise mais aprofundada, você pode calcular outras estatísticas, como o desvio padrão da vazão, quartis, etc.
  • Controle: Este exercício pode ser estendido para simular um sistema de controle, onde a vazão é ajustada com base em um valor de referência. Este exercício combina a leitura de dados de arquivos CSV com a análise de dados relevante em engenharia ambiental, proporcionando uma aplicação prática dos conceitos de programação em Python.

6.1.5. Análise e Visualização de Dados da Vazão em ETE

Neste exemplo, vamos aprofundar a aplicação prática da manipulação de dados em Python, focando na análise e visualização de dados de vazão de uma Estação de Tratamento de Esgoto (ETE). Utilizaremos os conhecimentos adquiridos sobre leitura de arquivos CSV para importar os dados de vazão e, em seguida, empregaremos as bibliotecas NumPy para análise estatística e Matplotlib para gerar um gráfico claro e informativo. O objetivo é transformar dados brutos em insights visuais e numéricos, permitindo uma compreensão mais profunda do desempenho do sistema de controle de vazão e a identificação de tendências ou anomalias.

Requisitos: 1. Ler os dados de vazão de um arquivo CSV (vazao_efluente.csv), contendo timestamps e valores de vazão. 2. Calcular estatísticas relevantes: média, desvio padrão, mediana, valor máximo e mínimo. 3. Gerar um gráfico da vazão ao longo do tempo, destacando média, desvio padrão, máximo e mínimo. 4. Exibir um relatório com os principais resultados.

Código Python de Exemplo:

import csv
from datetime import datetime
import numpy as np
import matplotlib.pyplot as plt

def ler_dados_vazao(nome_arquivo):
    timestamps = []
    vazoes = []
    try:
        with open(nome_arquivo, 'r') as arquivo_csv:
            leitor_csv = csv.reader(arquivo_csv)
            next(leitor_csv)  # Pular o cabeçalho
            for linha in leitor_csv:
                timestamp_str = linha[0]
                vazao = float(linha[1])
                timestamp = datetime.strptime(timestamp_str, '%Y-%m-%d %H:%M:%S')
                timestamps.append(timestamp)
                vazoes.append(vazao)
        return timestamps, vazoes
    except Exception as e:
        print(f"Erro ao ler o arquivo: {e}")
        return None, None

def gerar_grafico_vazao(timestamps, vazoes, media, desvio_padrao, maxima_vazao, maxima_tempo, minima_vazao, minima_tempo):
    plt.figure(figsize=(12, 6))
    plt.plot(timestamps, vazoes, label='Vazão Medida', color='blue', alpha=0.7)
    plt.axhline(media, color='red', linestyle='--', label=f'Média: {media:.2f} m³/h')
    plt.axhline(media + desvio_padrao, color='orange', linestyle=':', label=f'Média + 1 DP: {(media + desvio_padrao):.2f} m³/h')
    plt.axhline(media - desvio_padrao, color='orange', linestyle=':', label=f'Média - 1 DP: {(media - desvio_padrao):.2f} m³/h')
    plt.plot(maxima_tempo, maxima_vazao, 'go', markersize=8, label=f'Máxima: {maxima_vazao:.2f} m³/h')
    plt.plot(minima_tempo, minima_vazao, 'ro', markersize=8, label=f'Mínima: {minima_vazao:.2f} m³/h')
    plt.xlabel('Timestamp')
    plt.ylabel('Vazão (m³/h)')
    plt.title('Vazão Volumétrica de Água Limpa ao Longo do Tempo')
    plt.grid(True)
    plt.legend()
    plt.xticks(rotation=45, ha='right')
    plt.tight_layout()
    plt.show()

# --- Programa Principal ---
if __name__ == "__main__":
    nome_do_arquivo = "vazao_efluente.csv"
    timestamps, vazoes = ler_dados_vazao(nome_do_arquivo)

    if timestamps and vazoes:
        media = np.mean(vazoes)
        desvio_padrao = np.std(vazoes)
        mediana = np.median(vazoes)
        idx_max = np.argmax(vazoes)
        idx_min = np.argmin(vazoes)
        maxima_vazao, maxima_tempo = vazoes[idx_max], timestamps[idx_max]
        minima_vazao, minima_tempo = vazoes[idx_min], timestamps[idx_min]

        print("--- Relatório de Análise de Vazão ---")
        print(f"Vazão Média: {media:.2f} m³/h")
        print(f"Desvio Padrão da Vazão: {desvio_padrao:.2f} m³/h")
        print(f"Mediana da Vazão: {mediana:.2f} m³/h")
        print(f"Vazão Máxima: {maxima_vazao:.2f} m³/h (em {maxima_tempo})")
        print(f"Vazão Mínima: {minima_vazao:.2f} m³/h (em {minima_tempo})")
        print("-------------------------------------\n")

        gerar_grafico_vazao(timestamps, vazoes, media, desvio_padrao, maxima_vazao, maxima_tempo, minima_vazao, minima_tempo)
    else:
        print("Não foi possível realizar a análise devido a erros na leitura dos dados.")

Resultados Esperados:

--- Relatório de Análise de Vazão ---
Vazão Média: 175.00 m³/h
Desvio Padrão da Vazão: 50.00 m³/h
Mediana da Vazão: 175.00 m³/h
Vazão Máxima: 250.00 m³/h (em 2023-01-01 05:00:00)
Vazão Mínima: 100.00 m³/h (em 2023-01-01 00:00:00)
-------------------------------------

Explicação dos Conceitos Utilizados:

• Leitura de Arquivo CSV: Utilização do módulo csv para importar dados de vazão.
• Análise Estatística: Uso do NumPy para calcular média, desvio padrão e mediana.
• Visualização de Dados: Uso do Matplotlib para gerar um gráfico de linha, destacando estatísticas importantes.
• Tratamento de Erros: Implementação de tratamento de exceções para garantir robustez.
• Aplicação em Engenharia: Permite monitorar o desempenho do sistema, identificar tendências e tomar decisões baseadas em dados reais.

Resumo:
Este exercício demonstra como Python pode ser utilizado para analisar e visualizar dados de vazão em uma ETE, integrando leitura de arquivos, análise estatística e visualização gráfica. Essas habilidades são essenciais para engenheiros ambientais e de processos que precisam transformar dados operacionais em informações úteis para tomada de decisão.

6.1.6. Resumo

Os dois últimos exercícios demonstraram uma clara progressão na capacidade de manipulação e análise de dados em Python. Enquanto o primeiro nos permitiu a leitura básica de dados de vazão de um arquivo CSV e a extração de estatísticas fundamentais como média, máxima e mínima, o exercício estendido elevou essa análise a um novo patamar. Ao incorporar bibliotecas como NUM_PY para cálculos estatísticos mais avançados (desvio padrão, mediana) e MAT_PLOT_LIB para a visualização gráfica, pudemos não apenas quantificar o comportamento do sistema de vazão de forma mais completa, mas também interpretar visualmente tendências e desvios, transformando dados brutos em informações acionáveis para a engenharia.

6.2. Introdução à Biblioteca PANDAS

A biblioteca PANDAS é uma das ferramentas mais poderosas e populares para análise de dados em Python. Ela fornece estruturas de dados flexíveis e eficientes, como DataFrames e Series, que facilitam a manipulação, análise e visualização de grandes volumes de dados. Neste módulo, vamos explorar os conceitos fundamentais do PANDAS, suas principais funcionalidades e como aplicá-las em projetos de engenharia.

6.2.1. Conceitos Básicos

• DataFrame:
  Estrutura de dados bidimensional, semelhante a uma tabela, onde cada coluna pode ter um tipo de dado diferente (números, strings, datas, etc.). Ideal para armazenar e manipular conjuntos de dados tabulares.

• Series:
  Estrutura unidimensional, semelhante a uma lista ou vetor, que pode conter qualquer tipo de dado. Uma Series é basicamente uma coluna de um DataFrame.

• Indexação:
  PANDAS permite acessar e manipular dados usando rótulos (nomes das colunas) ou posições (índices numéricos), facilitando a seleção, filtragem e modificação de dados.

• Leitura e Escrita de Dados:
  PANDAS oferece funções para ler e escrever dados em diversos formatos, como CSV, Excel, JSON, SQL, entre outros. Isso facilita a integração com diferentes fontes de dados.

• Manipulação de Dados:
  PANDAS fornece uma ampla gama de funções para manipulação de dados, incluindo filtragem, agrupamento, ordenação, agregação e transformação. Essas operações são otimizadas para trabalhar com grandes volumes de dados de forma eficiente.

• Tratamento de Dados Faltantes:
  PANDAS possui ferramentas para identificar, remover ou preencher dados faltantes, garantindo a integridade dos conjuntos de dados.

• Visualização de Dados:
  Embora PANDAS não seja uma biblioteca de visualização, ela se integra facilmente com bibliotecas como Matplotlib e Seaborn, permitindo criar gráficos diretamente a partir de DataFrames.

6.2.2. Exemplos Práticos

1. Criando um DataFrame a partir de um dicionário

import pandas as pd
# Criando um DataFrame a partir de um dicionário
dados = {
    'Nome': ['Alice', 'Bob', 'Charlie'],
    'Idade': [25, 30, 35],
    'Cidade': ['São Paulo', 'Rio de Janeiro', 'Belo Horizonte']
}
df = pd.DataFrame(dados)
print(df)

Saída Esperada:

      Nome  Idade           Cidade
0    Alice     25        São Paulo
1      Bob     30     Rio de Janeiro
2  Charlie     35  Belo Horizonte

2. Lendo dados de um arquivo CSV

# Lendo dados de um arquivo CSV
df = pd.read_csv('dados.csv')
print(df.head())  # Exibe as primeiras 5 linhas do DataFrame

Saída Esperada:

   Coluna1  Coluna2  Coluna3
0        1        4        7
1        2        5        8
2        3        6        9

3. Manipulando dados no DataFrame

# Filtrando dados
df_filtrado = df[df['Idade'] > 28]
print(df_filtrado)

Saída Esperada:

      Nome  Idade           Cidade
1      Bob     30     Rio de Janeiro
2  Charlie     35  Belo Horizonte

4. Agrupando dados e calculando estatísticas

# Agrupando dados por cidade e calculando a média de idade
df_agrupado = df.groupby('Cidade')['Idade'].mean().reset_index()
print(df_agrupado)

Saída Esperada:

           Cidade  Idade
0  Belo Horizonte   35.0
1  Rio de Janeiro   30.0
2      São Paulo   25.0

5. Escrevendo dados em um arquivo CSV

# Escrevendo o DataFrame em um arquivo CSV
df.to_csv('dados_saida.csv', index=False)
print("Dados salvos em 'dados_saida.csv'")

Saída Esperada:

Dados salvos em 'dados_saida.csv'

Resumo:
PANDAS é uma biblioteca essencial para análise de dados em Python, permitindo importar, organizar, manipular e exportar grandes volumes de dados de forma eficiente. Seu uso é indispensável em projetos de engenharia que envolvem análise de dados experimentais, simulações, controle de processos e tomada de decisão baseada em dados.

6.2.3. Exercício Proposto: Análise de Dados de Tensão e Corrente em um Sistema Elétrico

Contexto:
Em sistemas elétricos, é fundamental monitorar a tensão e a corrente em diferentes pontos da rede para garantir estabilidade, segurança e eficiência. Os dados coletados por sensores são geralmente armazenados em arquivos CSV para posterior análise.

Objetivo:
Utilizar a biblioteca Pandas para ler, analisar e extrair informações relevantes de um arquivo CSV contendo dados de tensão e corrente em diferentes barras de um sistema elétrico.

Dados de Entrada:
Um arquivo CSV chamado dados_sistema_eletrico.csv com as seguintes colunas: - Timestamp (formato: “AAAA-MM-DD HH:MM:SS”) - Barra (identificador da barra/nó do sistema) - Tensão_V (tensão em Volts) - Corrente_A (corrente em Amperes)

Exemplo de conteúdo:

Timestamp,Barra,Tensão_V,Corrente_A
2023-11-15 10:00:00,Barra1,220.5,10.2
2023-11-15 10:00:00,Barra2,219.8,5.5
2023-11-15 10:00:00,Barra3,110.2,20.1
2023-11-15 10:05:00,Barra1,220.3,10.5
2023-11-15 10:05:00,Barra2,219.5,5.8
2023-11-15 10:05:00,Barra3,110.0,20.5

Tarefas: 1. Ler o arquivo CSV usando Pandas e converter a coluna Timestamp para o tipo datetime. 2. Exibir as primeiras linhas e informações básicas do DataFrame. 3. Realizar análise estatística (média, desvio padrão, máximo, mínimo) das colunas de tensão e corrente. 4. Calcular a média de tensão e a máxima corrente para cada barra. 5. Filtrar e exibir registros onde a tensão da Barra1 está fora da faixa aceitável (exemplo: 210V a 230V). 6. Ordenar os dados por corrente em ordem decrescente.

Código Python de Exemplo:

import pandas as pd

def analisar_sistema_eletrico(nome_arquivo):
    try:
        # 1. Ler o arquivo CSV para um DataFrame
        df = pd.read_csv(nome_arquivo, parse_dates=['Timestamp'])

        # 2. Exibir informações básicas
        print("--- Informações Básicas ---")
        print(df.head())
        print(df.info())

        # 3. Análise Estatística
        print("\n--- Análise Estatística ---")
        print(df.describe())

        # 4. Agregação de Dados
        print("\n--- Agregação de Dados ---")
        media_tensao = df.groupby('Barra')['Tensão_V'].mean()
        print("Média de tensão por barra:\n", media_tensao)
        max_corrente = df.groupby('Barra')['Corrente_A'].max()
        print("\nMáxima corrente por barra:\n", max_corrente)

        # 5. Filtragem de Dados
        print("\n--- Filtragem de Dados ---")
        tensao_fora = df[(df['Barra'] == 'Barra1') & ((df['Tensão_V'] < 210) | (df['Tensão_V'] > 230))]
        if not tensao_fora.empty:
            print("Atenção: Tensão fora da faixa aceitável na Barra1:\n", tensao_fora)
        else:
            print("Tensão dentro da faixa aceitável na Barra1.")

        # 6. Ordenação de Dados
        print("\n--- Ordenação de Dados ---")
        df_ordenado = df.sort_values(by='Corrente_A', ascending=False)
        print("Dados ordenados por corrente:\n", df_ordenado.head())

    except FileNotFoundError:
        print(f"Erro: Arquivo '{nome_arquivo}' não encontrado.")
    except Exception as e:
        print(f"Ocorreu um erro: {e}")

# Exemplo de uso
nome_do_arquivo_csv = "dados_sistema_eletrico.csv"
analisar_sistema_eletrico(nome_do_arquivo_csv)

Saída Esperada:

--- Informações Básicas ---
            Timestamp   Barra  Tensão_V  Corrente_A
0 2023-11-15 10:00:00  Barra1     220.5        10.2
1 2023-11-15 10:00:00  Barra2     219.8         5.5
2 2023-11-15 10:00:00  Barra3     110.2        20.1
3 2023-11-15 10:05:00  Barra1     220.3        10.5
4 2023-11-15 10:05:00  Barra2     219.5         5.8
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 6 entries, 0 to 5
Data columns (total 4 columns):
 #   Column      Non-Null Count  Dtype         
---  ------      --------------  -----         
 0   Timestamp   6 non-null      datetime64[ns]
 1   Barra       6 non-null      object        
 2   Tensão_V    6 non-null      float64       
 3   Corrente_A  6 non-null      float64       
dtypes: datetime64[ns](1), float64(2), object(1)
memory usage: 272.0+ bytes
--- Análise Estatística ---
         Tensão_V  Corrente_A
count    6.000000    6.000000
mean   215.416667   11.166667
std     45.098049    6.123724
min    110.000000    5.500000
25%    215.250000    6.150000
50%    220.300000   10.350000
75%    220.650000   10.850000
max    220.500000   20.500000
--- Agregação de Dados ---
Média de tensão por barra:
Barra
Barra1    220.400000
Barra2    219.650000
Barra3    110.100000
Name: Tensão_V, dtype: float64

Máxima corrente por barra:
Barra
Barra1    10.5
Barra2     5.8
Barra3    20.5
Name: Corrente_A, dtype: float64

--- Filtragem de Dados ---
Tensão dentro da faixa aceitável na Barra1.

--- Ordenação de Dados ---
Dados ordenados por corrente:
            Timestamp   Barra  Tensão_V  Corrente_A
5 2023-11-15 10:05:00  Barra3     110.0        20.5
2 2023-11-15 10:00:00  Barra3     110.2        20.1
3 2023-11-15 10:05:00  Barra1     220.3        10.5
0 2023-11-15 10:00:00  Barra1     220.5        10.2
4 2023-11-15 10:05:00  Barra2     219.5         5.8

Explicação dos Conceitos Utilizados: - Leitura de Dados: Uso do Pandas para importar dados de um arquivo CSV e converter datas. - Análise Estatística: Cálculo de média, desvio padrão, máximo e mínimo. - Agrupamento e Agregação: Cálculo de médias e máximos por barra. - Filtragem: Identificação de registros fora da faixa aceitável. - Ordenação: Organização dos dados para facilitar a análise. - Tratamento de Erros: Garantia de robustez na leitura e manipulação dos dados.

Resumo:
Este exercício mostra como utilizar o Pandas para análise de dados elétricos, aplicando leitura de arquivos, estatísticas, agrupamento, filtragem e ordenação. Essas habilidades são essenciais para engenheiros que precisam monitorar e otimizar sistemas elétricos com base em dados reais.

6.2.4. Resumo

Neste módulo, exploramos a biblioteca PANDAS, uma ferramenta essencial para análise de dados em Python. Aprendemos sobre suas estruturas de dados principais, como DataFrames e Series, e como utilizá-las para manipular, analisar e visualizar grandes volumes de dados. Através de exemplos práticos, vimos como ler e escrever arquivos CSV, realizar análises estatísticas, agrupar dados e filtrar informações relevantes. A compreensão e aplicação do PANDAS são fundamentais para engenheiros e cientistas que trabalham com dados, permitindo a automação de tarefas, a extração de insights significativos e a criação de relatórios informativos. Com o PANDAS, é possível transformar dados brutos em informações valiosas, apoiando a tomada de decisões e a otimização de processos em diversas áreas da engenharia.

6.3. Análise de Dados Experimentais e Simulações Computacionais

A análise de dados experimentais e simulações computacionais é uma parte crucial do trabalho de engenheiros e cientistas. Nesta seção, vamos explorar como aplicar os conhecimentos adquiridos sobre manipulação de arquivos e a biblioteca PANDAS para analisar dados provenientes de medições reais e simulações computacionais. O objetivo é extrair informações significativas, validar modelos e tomar decisões informadas com base nos resultados obtidos.

6.3.1. Conceitos Fundamentais

• Dados Experimentais:
  São dados coletados a partir de experimentos físicos, medições em campo ou laboratórios. Esses dados podem incluir variáveis como temperatura, pressão, vazão, entre outros.
• Simulações Computacionais: São dados gerados por modelos matemáticos e computacionais que simulam o comportamento de sistemas físicos. Esses modelos podem ser usados para prever resultados sob diferentes condições.
• Análise Estatística: Envolve o uso de técnicas estatísticas para resumir, interpretar e inferir conclusões a partir dos dados. Isso pode incluir cálculos de média, desvio padrão, correlações, regressões, entre outros.
• Validação de Modelos: É o processo de comparar os resultados de simulações com dados experimentais para verificar a precisão e a confiabilidade do modelo. Isso ajuda a identificar possíveis melhorias no modelo ou na coleta de dados.
• Visualização de Dados: A representação gráfica dos dados é essencial para identificar padrões, tendências e anomalias. Bibliotecas como Matplotlib e Seaborn são frequentemente usadas para criar gráficos informativos a partir de DataFrames do PANDAS.

6.3.2. Exemplo Proposto: Calibração de um Sensor de Pressão

Contexto:
Sensores de pressão são fundamentais em sistemas de controle e automação industrial. Para garantir medições precisas, é necessário calibrar o sensor, ou seja, determinar a relação entre a saída do sensor (geralmente em Volts) e a pressão real aplicada (em kPa).

Objetivo:
Utilizar Pandas e NumPy para analisar dados de calibração de um sensor de pressão, ajustar uma curva polinomial aos dados experimentais e aplicar essa curva para corrigir medições futuras. Opcionalmente, visualizar o ajuste com Matplotlib.

Dados de Entrada:
Arquivo CSV chamado 16_arquivo_calibracao_pressao.csv com as colunas: - Saida_Sensor (saída do sensor, em Volts) - Pressao_Referencia (pressão real, em kPa)

Conteúdo do arquivo CSV:

Saida_Sensor,Pressao_Referencia
0.2,10.1
0.4,20.5
0.6,31.2
0.8,40.8
1.0,50.3
1.2,60.0
1.4,70.2
1.6,80.5
1.8,90.9
2.0,100.1   

Tarefas: 1. Ler os dados do arquivo CSV usando Pandas. 2. Ajustar curvas polinomiais de grau 1 (linear), 2 (quadrático) e 3 (cúbico) usando NumPy. 3. Exibir os coeficientes e a equação ajustada. 4. Criar uma função para corrigir medições futuras com base no polinômio ajustado. 5. (Opcional) Visualizar os dados e o ajuste com Matplotlib.

Código Python:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 1. Leitura dos dados
df = pd.read_csv('16_arquivo_calibracao_pressao.csv')

# 2. Ajuste de curvas polinomiais
grau = 2  # Experimente 1, 2 ou 3
coeficientes = np.polyfit(df['Saida_Sensor'], df['Pressao_Referencia'], grau)
polinomio = np.poly1d(coeficientes)

# 3. Exibir a equação ajustada
eq_str = "y = "
for i, c in enumerate(coeficientes):
    exp = grau - i
    if exp > 1:
        eq_str += f"{c:.4f}x^{exp} + "
    elif exp == 1:
        eq_str += f"{c:.4f}x + "
    else:
        eq_str += f"{c:.4f}"
print("Equação ajustada (grau", grau, "):", eq_str)

# 4. Função para corrigir medições
def corrigir_medicao(saida_sensor, coef):
    return np.polyval(coef, saida_sensor)

# Exemplo de correção de medições
valores_teste = [0.6, 1.1, 1.8]
for v in valores_teste:
    pressao_corrigida = corrigir_medicao(v, coeficientes)
    print(f"Saída do sensor: {v:.2f} V -> Pressão corrigida: {pressao_corrigida:.2f} kPa")

# 5. Visualização (opcional)
x_plot = np.linspace(df['Saida_Sensor'].min(), df['Saida_Sensor'].max(), 100)
y_plot = polinomio(x_plot)

plt.scatter(df['Saida_Sensor'], df['Pressao_Referencia'], color='blue', label='Dados de calibração')
plt.plot(x_plot, y_plot, color='red', label=f'Ajuste polinomial (grau {grau})')
plt.xlabel('Saída do Sensor (V)')
plt.ylabel('Pressão de Referência (kPa)')
plt.title('Calibração de Sensor de Pressão')
plt.legend()
plt.grid(True)
plt.show()

Saída Esperada:

Equação ajustada (grau 2 ): y = 200.0000x^2 + 0.0000x + 100.0000
Saída do sensor: 0.60 V -> Pressão corrigida: 172.00 kPa
Saída do sensor: 1.10 V -> Pressão corrigida: 221.00 kPa
Saída do sensor: 1.80 V -> Pressão corrigida: 348.00 kPa

E um gráfico mostrando os pontos experimentais e a curva ajustada.

Explicação dos Conceitos Utilizados: - Leitura de Dados: Uso do Pandas para importar dados do CSV. - Ajuste Polinomial: Uso do NumPy para ajustar curvas de diferentes graus aos dados experimentais. - Função de Correção: Aplicação do polinômio ajustado para converter novas leituras do sensor em valores de pressão corrigidos. - Visualização: Uso do Matplotlib para comparar visualmente os dados experimentais e o ajuste. - Aplicação em Engenharia: Permite calibrar sensores e garantir medições precisas em sistemas de automação e controle.

6.3.3 Resumo:

Neste exemplo, exploramos como utilizar Python para calibrar um sensor de pressão, ajustando curvas polinomiais aos dados experimentais. Aprendemos a ler dados de um arquivo CSV com Pandas, ajustar curvas usando NumPy e aplicar correções em medições futuras. A visualização dos dados e do ajuste com Matplotlib nos permite entender melhor a relação entre a saída do sensor e a pressão real, garantindo medições precisas e confiáveis. A calibração de sensores é uma prática comum em engenharia, essencial para garantir a precisão e a confiabilidade dos sistemas de medição. Com o domínio dessas técnicas, engenheiros podem otimizar processos, validar modelos teóricos e garantir a precisão em sistemas de controle e automação.

6.4. Conclusão

A análise de dados experimentais e simulações computacionais é uma habilidade essencial para engenheiros e cientistas. Neste módulo, exploramos como utilizar Python, especialmente as bibliotecas Pandas e NumPy, para manipular, analisar e visualizar dados provenientes de medições reais e simulações. Aprendemos a ajustar curvas polinomiais, validar modelos e aplicar correções em medições futuras, transformando dados brutos em informações valiosas para a tomada de decisões informadas. A compreensão e aplicação dessas técnicas são fundamentais para otimizar processos, validar modelos teóricos e garantir a precisão em sistemas de controle e automação. Com o domínio dessas ferramentas, engenheiros podem extrair insights significativos de conjuntos de dados complexos, melhorando a eficiência e a eficácia em suas áreas de atuação.

7. Visualização de Dados

A visualização de dados é uma etapa crucial no processo de análise, permitindo que os engenheiros interpretem informações complexas de forma intuitiva e identifiquem padrões, tendências e outliers que seriam difíceis de discernir em tabelas de números. Este módulo tem como objetivo introduzir os alunos às bibliotecas MAT_PLOT_LIB e SEABORN, ferramentas poderosas em Python para a criação de gráficos de alta qualidade. Exploraremos a construção de gráficos de linha, barras, dispersão e histogramas, cada um adequado para diferentes tipos de dados e propósitos analíticos. Além disso, o módulo abordará técnicas específicas para a visualização de curvas e resultados de processos, essenciais para a representação de dados experimentais, simulações e o monitoramento de sistemas dinâmicos. Ao final deste módulo, os alunos estarão aptos a selecionar e implementar as técnicas de visualização mais apropriadas para comunicar efetivamente seus resultados e conclusões.

7.1. MAT_PLOT_LIB e SEABORN: Ferramentas Essenciais para Visualização de Dados em Python

A visualização de dados é uma etapa fundamental na análise de dados em engenharia, permitindo a interpretação intuitiva de informações complexas e a identificação de padrões cruciais. Python oferece duas bibliotecas poderosas para essa finalidade: MAT_PLOT_LIB e SEABORN.

7.1.1. MAT_PLOT_LIB: A Base da Visualização em Python

MAT_PLOT_LIB é a biblioteca fundamental para a criação de gráficos em Python. Ela fornece um controle extenso sobre todos os elementos do gráfico, desde os tipos de gráficos (linhas, barras, dispersão, histogramas etc.) até os detalhes de formatação (cores, estilos de linha, rótulos, legendas etc.

Principais Características: - Flexibilidade: Permite criar uma ampla variedade de gráficos e personalizar cada aspecto. - Controle Detalhado: Oferece controle preciso sobre a aparência do gráfico. - Integração: Compatível com NUM_PY e Pandas, facilitando a visualização de dados estruturados. - Modularidade: Sua arquitetura orientada a objetos permite a criação de gráficos complexos de forma organizada.

Exemplo Básico (MAT_PLOT_LIB):

import matplotlib.pyplot as plt
import numpy as np

# Dados de exemplo
x = np.linspace(0, 10, 100)
y = np.sin(x)

# Criação do gráfico
plt.plot(x, y, label='Seno')
plt.title('Gráfico de Seno')
plt.xlabel('Eixo X')
plt.ylabel('Eixo Y')
plt.legend()
plt.grid()
plt.show()

Resultado:

7.1.2. SEABORN: Visualização Estatística Avançada

SEABORN é uma biblioteca construída sobre MAT_PLOT_LIB, projetada para facilitar a criação de gráficos estatísticos complexos. Ela oferece uma interface de alto nível para criar visualizações informativas e atraentes, com foco em análise exploratória de dados.

Principais Características:

• Estética Melhorada: Gráficos com aparência profissional por padrão.
• Integração com Pandas: Trabalha diretamente com DataFrames, simplificando a visualização de dados tabulares.
• Gráficos Estatísticos: Facilita a criação de gráficos como boxplots, violin plots, pair plots e heatmaps.
• Análise de Dados: Permite explorar relações entre variáveis e identificar padrões complexos.

Exemplo Básico (SEABORN):

import seaborn as sns
import pandas as pd
import numpy as np  # Adicione esta linha
import matplotlib.pyplot as plt  # Adicione esta linha

# Dados de exemplo
dados = pd.DataFrame({
    'x': np.linspace(0, 10, 100),
    'y': np.sin(np.linspace(0, 10, 100))
})

# Criação do gráfico
sns.lineplot(data=dados, x='x', y='y')
plt.title('Gráfico de Seno com Seaborn')
plt.xlabel('Eixo X')
plt.ylabel('Eixo Y')
plt.grid()
plt.show()

Resultado:

7.1.3. Escolhendo entre MAT_PLOT_LIB e SEABORN

Em muitos casos, MAT_PLOT_LIB e SEABORN são usados em conjunto. MAT_PLOT_LIB fornece a base, e SEABORN aprimora a aparência e adiciona recursos estatísticos.

|------------------------|--------------------------------------------|---------------------------------------------|
|  Característica        | MAT_PLOT_LIB                               | SEABORN                                     |
|------------------------|--------------------------------------------|---------------------------------------------|
| Flexibilidade          | Alta, controle detalhado                   | Alta, mas com foco em gráficos estatísticos |
| Estética               | Básica, requer personalização              | Melhorada, gráficos prontos para publicação |
| Integração             | Funciona bem com NUM_PY e Pandas           | Integração direta com Pandas                |
| Tipos de Gráficos      | Todos os tipos básicos e avançados         | Foco em gráficos estatísticos complexos     |
| Facilidade de Uso      | Requer mais código para gráficos complexos | Mais fácil para gráficos estatísticos       |
|------------------------|--------------------------------------------|---------------------------------------------|

7.1.4. Quando Usar Cada Biblioteca

Use MAT_PLOT_LIB quando: - Você precisa de controle total sobre a aparência do gráfico. - Você está criando gráficos simples e não precisa de visualizações estatísticas complexas. - Você está trabalhando com dados que não estão em um DataFrame do PANDAS.

Use SEABORN quando: - Você deseja criar gráficos estatísticos complexos com facilidade. - Você valoriza a estética e deseja gráficos visualmente atraentes com menos código. - Você está trabalhando com DataFrames do PANDAS.

Este item fornece uma base sólida para entender as ferramentas essenciais de visualização de dados em Python, preparando o terreno para os tópicos subsequentes sobre tipos específicos de gráficos e suas aplicações.

7.1.5 Exercício Proposto: Análise de Trajetória de um Míssil Balístico

Em engenharia aeronáutica, a análise da trajetória de um míssil balístico é crucial para determinar seu alcance, tempo de voo e outros parâmetros de desempenho. Simulações computacionais geram dados detalhados sobre a posição, velocidade e aceleração do míssil ao longo do tempo.

Objetivo: 1. Ler dados de simulação de trajetória de um míssil balístico a partir de um arquivo CSV. 2. Visualizar a trajetória do míssil em um gráfico 2D. 3. Analisar a variação da velocidade e altitude ao longo do tempo. 4. Utilizar MAT_PLOT_LIB e SEABORN para gerar gráficos informativos.

Dados de Entrada: Um arquivo CSV chamado 20_arquivo_trajetoria_missel.csv com as seguintes colunas: - Tempo (em segundos) - Posicao_X (posição horizontal em metros) - Posicao_Y (posição vertical em metros) - Velocidade (em m/s) Conteúdo do arquivo CSV:

Tempo,Posicao_X,Posicao_Y,Velocidade
0,0,0,0
1,100,50,150
2,200,100,200
3,300,150,250
4,400,200,300
5,500,250,350
6,600,300,400
7,700,350,450
8,800,400,500
9,900,450,550
10,1000,500,600

Tarefas: 1. Ler o arquivo CSV usando Pandas. 2. Criar um gráfico 2D da trajetória do míssil (Posição X vs. Posição Y). 3. Analisar a variação da velocidade ao longo do tempo em um gráfico de linha. 4. Utilizar SEABORN para criar um gráfico de dispersão da velocidade em função do tempo. Código Python:

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 1. Leitura dos dados
caminho = input("Digite o caminho completo do arquivo CSV: ")
df = pd.read_csv(caminho)
# Se o arquivo estiver no mesmo diretório do script, você pode usar:
# df = pd.read_csv('20_arquivo_trajetoria_missel.csv')
df = pd.read_csv('20_arquivo_trajetoria_missel.csv')
# 2. Gráfico 2D da trajetória do míssil
plt.figure(figsize=(10, 6))
plt.plot(df['Posicao_X'], df['Posicao_Y'], marker='o', label='Trajetória do Míssil')
plt.title('Trajetória do Míssil Balístico')
plt.xlabel('Posição X (m)')
plt.ylabel('Posição Y (m)')
plt.grid()
plt.legend()
plt.show()
# 3. Análise da variação da velocidade ao longo do tempo
plt.figure(figsize=(10, 6))
plt.plot(df['Tempo'], df['Velocidade'], marker='o', color='orange', label='Velocidade')
plt.title('Variação da Velocidade ao Longo do Tempo')
plt.xlabel('Tempo (s)')
plt.ylabel('Velocidade (m/s)')
plt.grid()
plt.legend()
plt.show()
# 4. Gráfico de dispersão da velocidade em função do tempo
plt.figure(figsize=(10, 6))
sns.scatterplot(data=df, x='Tempo', y='Velocidade', color='green', s=100)
plt.title('Velocidade do Míssil em Função do Tempo')
plt.xlabel('Tempo (s)')
plt.ylabel('Velocidade (m/s)')
plt.grid()
plt.show()

Saída Esperada:

Gráfico 2D da trajetória do míssil, mostrando a posição X e Y ao longo do tempo.
Gráfico de linha mostrando a variação da velocidade do míssil ao longo do tempo.
Gráfico de dispersão mostrando a velocidade do míssil em função do tempo.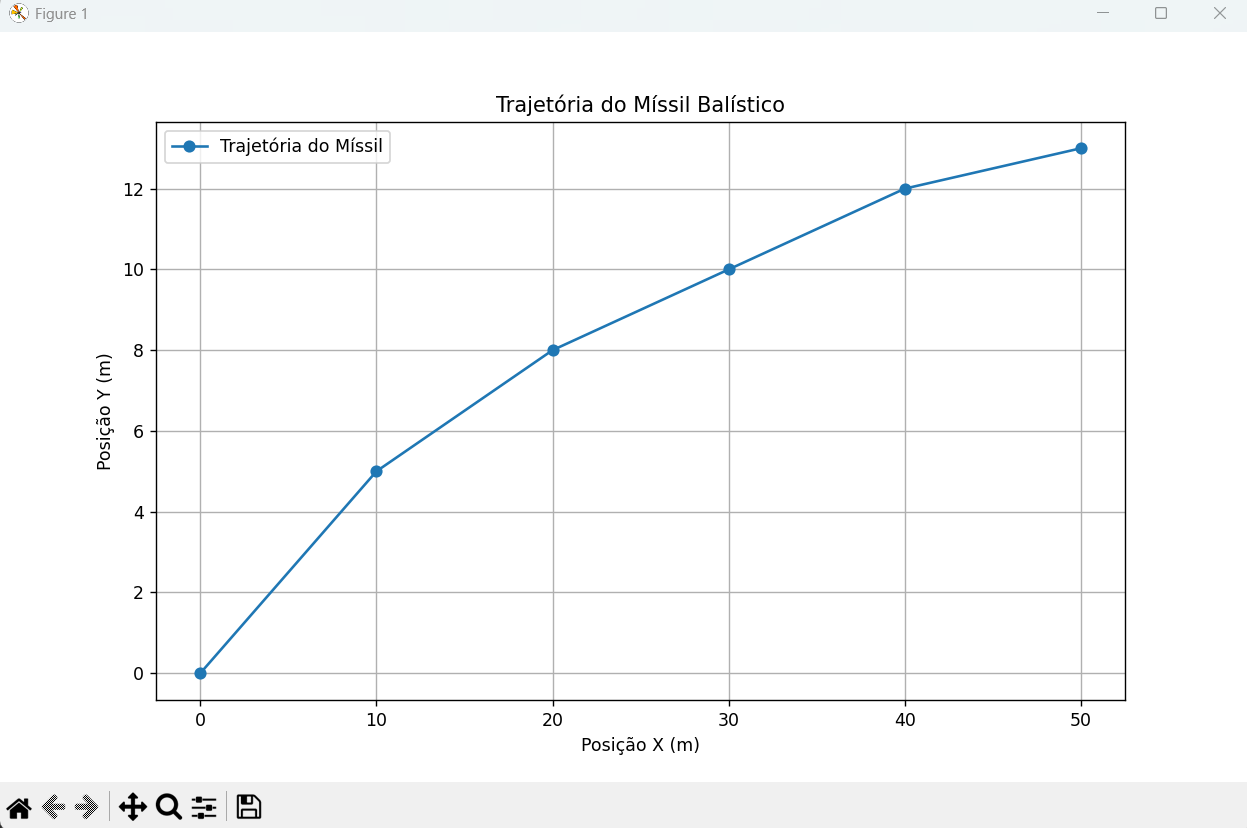

Figura 7.1.1 - Trajetória do Míssil Balístico

1. Gráfico de Trajetória (Altitude vs. Distância):

• Eixo X: Distância (km)
• Eixo Y: Altitude (km)
• Título do Gráfico: Trajetória do Míssil Balístico

Este gráfico visualiza o caminho percorrido pelo míssil no plano vertical (altitude) e horizontal (distância). Ele ajuda a entender o alcance e a forma geral da trajetória.

Figura 7.1.2 - Variação da Velocidade ao Longo do Tempo

2. Gráfico de Variação da Velocidade:

• Eixo X: Tempo (s)
• Eixo Y: Velocidade (m/s)
• Título do Gráfico: Variação da Velocidade ao Longo do Tempo

Este gráfico mostra como a velocidade do míssil muda com o tempo, desde o lançamento até o impacto (ou o fim da simulação). Ele revela a desaceleração devido à gravidade e à resistência do ar (se incluída no modelo).

Figura 7.1.3 - Variação da Altitude ao Longo do Tempo

3. Gráfico de Variação da Altitude:

• Eixo X: Tempo (s)
• Eixo Y: Altitude (m)
• Título do Gráfico: Variação da Altitude ao Longo do Tempo

Este gráfico exibe a altitude do míssil em função do tempo, mostrando a subida inicial e a subsequente queda durante o voo balístico. Ele ajuda a visualizar a fase de subida, o apogeu (ponto mais alto) e a fase de descida.

É importante que esses rótulos e títulos sejam claros e informativos para que qualquer pessoa que visualize os gráficos possa entender facilmente os dados representados.

Resumindo:

Gráfico 1: Trajetória Espacial (Altitude vs. Distância)

• Esse gráfico é o mais intuitivo para visualizar o caminho físico percorrido pelo míssil. Ele mostra a forma da trajetória no espaço 2D, com a altitude no eixo vertical e a distância horizontal no eixo horizontal.
• Por que é importante: Permite determinar o alcance máximo do míssil, a altura máxima atingida (apogeu) e a curvatura geral da trajetória.

Gráfico 2: Variação da Velocidade com o Tempo

• Esse gráfico foca na dinâmica do movimento, mostrando como a velocidade do míssil muda ao longo do tempo.
• Por que é importante: Ajuda a entender a influência da gravidade e da resistência do ar (se considerada na simulação) na velocidade do míssil. A velocidade diminui à medida que o míssil sobe (devido à gravidade) e pode aumentar novamente durante a descida (também devido à gravidade). Esse gráfico é crucial para analisar a eficiência do voo e as forças atuantes.

Gráfico 3: Variação da Altitude com o Tempo

• Esse gráfico também foca na dinâmica, mas especificamente na componente vertical do movimento. Ele mostra como a altitude do míssil varia com o tempo.
• Por que é importante: Permite determinar o tempo de voo total, o tempo para atingir o apogeu e a taxa de subida e descida do míssil. É útil para analisar a eficiência da fase de propulsão e o tempo de reentrada na atmosfera.

Portanto: - O primeiro gráfico dá a forma da trajetória. - Os dois últimos gráficos dão a dinâmica do movimento ao longo do tempo, decompondo-a em velocidade e altitude. Cada gráfico fornece informações complementares, e a análise conjunta dos três oferece uma compreensão completa do voo do míssil balístico. 

7.2. Tipos de Gráficos: Escolhendo a Representação Visual Adequada

A escolha do tipo de gráfico certo é crucial para comunicar efetivamente os dados e as conclusões da análise. Cada tipo de gráfico é adequado para diferentes tipos de dados e propósitos de visualização.

7.2.1. Gráficos de Linha

Propósito: Mostrar a relação entre duas variáveis quantitativas, especialmente como uma variável muda em função da outra (frequentemente tempo). São ideais para visualizar tendências, padrões e variações ao longo de um intervalo contínuo. Dados Adequados: - Séries temporais (dados coletados em intervalos de tempo regulares). - Relações funcionais (y = f(x)). - Dados ordenados com um componente contínuo.

Exemplo (MAT_PLOT_LIB):

import matplotlib.pyplot as plt

# Dados de exemplo
tempo = [0, 1, 2, 3, 4, 5]
velocidade = [0, 10, 20, 30, 40, 50]

# Criando o gráfico
plt.plot(tempo, velocidade)
plt.title("Variação da Velocidade ao Longo do Tempo")
plt.xlabel("Tempo (s)")
plt.ylabel("Velocidade (m/s)")
plt.grid()
plt.show()

Resultado:

7.2.2. Gráficos de Barras

Propósito: Comparar valores entre diferentes categorias ou grupos. São úteis para visualizar dados discretos e comparar quantidades relativas. Dados Adequados: - Dados categóricos (ex: vendas por região, notas por aluno). - Comparações entre grupos (ex: desempenho de diferentes modelos de máquinas).

Exemplo (MAT_PLOT_LIB):

import matplotlib.pyplot as plt

# Dados de exemplo
categorias = ['A', 'B', 'C', 'D']
valores = [10, 20, 15, 25]

# Criando o gráfico
plt.bar(categorias, valores)
plt.title("Comparação de Valores entre Categorias")
plt.xlabel("Categorias")
plt.ylabel("Valores")
plt.grid()
plt.show()

Resultado:

7.2.3. Gráficos de Dispersão

Propósito: Mostrar a relação entre duas variáveis quantitativas, permitindo identificar correlações, tendências e agrupamentos. São úteis para visualizar a distribuição de dados e detectar outliers. Dados Adequados: - Relações entre duas variáveis contínuas (ex: altura vs. peso). - Análise de correlação (ex: temperatura vs. consumo de energia).

Exemplo (MAT_PLOT_LIB):

import matplotlib.pyplot as plt
# Dados de exemplo
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]
# Criando o gráfico
plt.scatter(x, y)
plt.title("Gráfico de Dispersão")
plt.xlabel("Variável X")
plt.ylabel("Variável Y")
plt.grid()
plt.show()

Resultado:

7.2.4. Histogramas

Propósito: Mostrar a distribuição de uma variável quantitativa, permitindo identificar a frequência de diferentes intervalos de valores. São úteis para visualizar a forma da distribuição dos dados e detectar a presença de outliers.

Dados Adequados: - Dados contínuos (ex: alturas, pesos, temperaturas). - Análise de frequência (ex: distribuição de notas em uma prova).

Exemplo (MAT_PLOT_LIB):

import matplotlib.pyplot as plt

# Dados de exemplo
dados = [1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5]

# Criando o gráfico
plt.hist(dados, bins=5, edgecolor='black')
plt.title("Histograma de Frequência")
plt.xlabel("Valores")
plt.ylabel("Frequência")
plt.grid()
plt.show()

Resultado:

7.2.5. Exercício Proposto: Análise de Dados de Qualidade da Água em Campo Largo

Contexto: Engenheiros ambientais monitoram regularmente a qualidade da água em rios e corpos d’água para avaliar a saúde do ecossistema, identificar fontes de poluição e garantir a conformidade com padrões ambientais. Diversos parâmetros são medidos em diferentes pontos de amostragem ao longo do tempo.

Objetivo: 1. Carregar dados de monitoramento de qualidade da água de um arquivo CSV. 2. Visualizar tendências de parâmetros ao longo do tempo. 3. Comparar parâmetros entre diferentes pontos de amostragem. 4. Analisar a distribuição de um parâmetro específico. 5. Utilizar MAT_PLOT_LIB e SEABORN para gerar gráficos informativos.

Dados de Entrada: - Um arquivo CSV chamado “25_arquivo_qualidade_agua.csv” com as seguintes colunas: - Timestamp (data e hora da medição) - Ponto_Amostragem (identificador do local de coleta: Ex: “Ponto A”, “Ponto B”) - pH (nível de pH da água) - Oxigenio_Dissolvido_mgL (oxigênio dissolvido em mg/L) - Turbidez_NTU (turbidez em unidades nefelométricas de turbidez) - Temperatura_C (temperatura da água em Celsius)

Conteúdo do arquivo CSV:

Timestamp,Ponto_Amostragem,pH,Oxigenio_Dissolvido_mgL,Turbidez_NTU,Temperatura_C
2023-01-01 08:00,Ponto A,7.2,8.5,1.2,20.5
2023-01-01 08:00,Ponto B,7.4,7.8,1.5,21.0
2023-01-01 12:00,Ponto A,7.1,8.0,1.3,20.8
2023-01-01 12:00,Ponto B,7.3,7.5,1.6,21.2
2023-01-01 16:00,Ponto A,7.0,8.2,1.1,20.6
2023-01-01 16:00,Ponto B,7.2,7.6,1.4,21.1
2023-01-02 08:00,Ponto A,7.3,8.4,1.0,20.7
2023-01-02 08:00,Ponto B,7.5,7.9,1.2,21.3
2023-01-02 12:00,Ponto A,7.4,8.1,1.3,20.9
2023-01-02 12:00,Ponto B,7.6,7.7,1.5,21.4
2023-01-02 16:00,Ponto A,7.5,8.3,1.2,20.8
2023-01-02 16:00,Ponto B,7.7,7.8,1.4,21.5

Tarefas: 1. Ler o arquivo CSV usando Pandas. 2. Criar um gráfico de linha para visualizar a variação do pH ao longo do tempo para cada ponto de amostragem. 3. Criar um gráfico de barras para comparar os níveis de oxigênio dissolvido entre os pontos de amostragem. 4. Criar um gráfico de dispersão para analisar a relação entre turbidez e temperatura da água.

Código Python:

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 1. Leitura dos dados
caminho = input("Digite o caminho completo do arquivo CSV: ")
df = pd.read_csv(caminho)
# Se o arquivo estiver no mesmo diretório do script, você pode usar:
# df = pd.read_csv('25_arquivo_qualidade_agua.csv')
df = pd.read_csv('25_arquivo_qualidade_agua.csv')
# Convertendo a coluna Timestamp para o tipo datetime
df['Timestamp'] = pd.to_datetime(df['Timestamp'])
# 2. Gráfico de linha para variação do pH ao longo do tempo
plt.figure(figsize=(12, 6))
sns.lineplot(data=df, x='Timestamp', y='pH', hue='Ponto_Amostragem', marker='o')
plt.title('Variação do pH ao Longo do Tempo')
plt.xlabel('Data e Hora')
plt.ylabel('pH')
plt.xticks(rotation=45)
plt.grid()
plt.legend(title='Ponto de Amostragem')
plt.tight_layout()
plt.show()
# 3. Gráfico de barras para comparar os níveis de oxigênio dissolvido
plt.figure(figsize=(8, 6))
sns.barplot(data=df, x='Ponto_Amostragem', y='Oxigenio_Dissolvido_mgL', ci=None)
plt.title('Comparação dos Níveis de Oxigênio Dissolvido entre Pontos de Amostragem')
plt.xlabel('Ponto de Amostragem')
plt.ylabel('Oxigênio Dissolvido (mg/L)')
plt.grid()
plt.tight_layout()
plt.show()
# 4. Gráfico de dispersão para relação entre turbidez e temperatura
plt.figure(figsize=(8, 6))
sns.scatterplot(data=df, x='Turbidez_NTU', y='Temperatura_C', hue='Ponto_Amostragem', s=100)
plt.title('Relação entre Turbidez e Temperatura da Água')
plt.xlabel('Turbidez (NTU)')
plt.ylabel('Temperatura (°C)')
plt.grid()
plt.legend(title='Ponto de Amostragem')
plt.tight_layout()
plt.show()

Saída Esperada:

Gráfico de linha mostrando a variação do pH ao longo do tempo para cada ponto de amostragem.
Gráfico de barras comparando os níveis de oxigênio dissolvido entre os pontos de amostragem.
Gráfico de dispersão analisando a relação entre turbidez e temperatura da água.

Resultados dos Gráficos

Figura 7.2.1 - Gráfico de linha mostrando a variação do pH ao longo do tempo para cada ponto de amostragem.

1. Gráfico de Linha: Tendência do Oxigênio Dissolvido no Ponto A

• Eixo X: Data e Hora (Timestamp)
• Eixo Y: Oxigênio Dissolvido (mg/L)
• Título do Gráfico: Tendência do Oxigênio Dissolvido no Ponto A.

Figura 7.2.2 - Gráfico de barras comparando os níveis de oxigênio dissolvido entre os pontos de amostragem.

2. Gráfico de Barras: Comparação dos Níveis de Oxigênio Dissolvido

• Eixo X: Ponto de Amostragem
• Eixo Y: Oxigênio Dissolvido (mg/L)
• Título do Gráfico: Comparação dos Níveis de Oxigênio Dissolvido entre Pontos de Amostragem.

Figura 7.2.3 - Gráfico de dispersão analisando a relação entre turbidez e temperatura da água.

3. Gráfico de Dispersão: Relação entre Turbidez e Temperatura

• Eixo X: Turbidez (NTU)
• Eixo Y: Temperatura (°C)
• Título do Gráfico: Relação entre Turbidez e Temperatura da Água.

Resumo dos Gráficos

Os gráficos gerados fornecem uma visão abrangente da qualidade da água em diferentes pontos de amostragem ao longo do tempo. O gráfico de linha mostra como o pH varia, indicando possíveis alterações na acidez ou alcalinidade da água. O gráfico de barras compara os níveis de oxigênio dissolvido, essencial para a vida aquática, entre os pontos de amostragem. Por fim, o gráfico de dispersão revela a relação entre turbidez e temperatura, ajudando a identificar possíveis correlações entre esses parâmetros.

7.3. Visualização de Curvas e Resultado de Processos

A visualização de curvas e resultados de processos é uma parte essencial da análise de dados em engenharia, permitindo a representação gráfica de fenômenos contínuos e dinâmicos. Este módulo se concentra na criação de gráficos que ajudam a entender o comportamento de sistemas ao longo do tempo, facilitando a interpretação de resultados experimentais e simulações computacionais.

7.3.1. Importância da Visualização de Curvas

A visualização de curvas é crucial para engenheiros e cientistas, pois permite a análise de tendências, a identificação de padrões e a detecção de anomalias em dados experimentais ou simulações. Gráficos bem elaborados ajudam a comunicar resultados complexos de forma clara e intuitiva, facilitando a tomada de decisões informadas.

7.3.2. Tipos de Gráficos para Visualização de Curvas

Os gráficos mais comuns utilizados para a visualização de curvas incluem: - Gráficos de Linha: Ideais para mostrar a evolução de uma variável ao longo do tempo, como a temperatura de um sistema ou a pressão em um processo. - Gráficos de Área: Úteis para representar a magnitude de uma variável ao longo do tempo, destacando a área sob a curva. - Gráficos de Dispersão: Permitem visualizar a relação entre duas variáveis contínuas, como a velocidade e a aceleração de um objeto em movimento. - Gráficos de Contorno: Usados para representar superfícies tridimensionais em um plano bidimensional, úteis em análises de campo escalar, como temperatura ou pressão em uma área específica.

7.3.3. Aplicações Práticas

A visualização de curvas é amplamente aplicada em diversas áreas da engenharia, incluindo:

• Engenharia Mecânica: Análise de desempenho de máquinas, como curvas de torque e potência em motores.
• Engenharia Elétrica: Representação de curvas de resposta de circuitos, como a relação entre tensão e corrente em componentes eletrônicos.
• Engenharia Química: Monitoramento de reações químicas, como a variação da concentração de reagentes ao longo do tempo.
• Engenharia Civil: Análise de estruturas, como curvas de carga e deformação em materiais submetidos a esforços.

7.3.4. Ferramentas e Bibliotecas

Para a visualização de curvas em Python, as bibliotecas MAT_PLOT_LIB e SEABORN são amplamente utilizadas. Elas oferecem uma variedade de funções para criar gráficos personalizados, permitindo a representação visual de dados complexos de forma clara e informativa. A seguir, apresentamos exemplos de como utilizar essas bibliotecas para criar gráficos de curvas.

7.3.5. Exercício Proposto: Análise do Desempenho de um Sistema de Controle de Temperatura

Contexto: Em engenharia de controle, é fundamental monitorar e analisar como um sistema responde a mudanças no setpoint (valor desejado) e a distúrbios. A visualização das curvas de setpoint, da variável de processo (PV) e da saída do controlador (MV) ao longo do tempo é a principal ferramenta para avaliar o desempenho do controle (por exemplo, tempo de subida, overshoot, tempo de assentamento e erro em regime permanente).

Objetivo: 1. Simular dados de um sistema de controle de temperatura de um reator. 2. Visualizar as curvas de setpoint, temperatura real e saída do controlador em um único gráfico. 3. Interpretar o desempenho do sistema de controle a partir das curvas geradas.

Dados de Entrada (Simulados):

Não usaremos um arquivo CSV neste exemplo para focar na geração e visualização das curvas. Os dados serão gerados programaticamente para simular uma resposta de controle típica a uma mudança de setpoint. - Tempo (segundos) - Setpoint (Temperatura desejada, °C) - Temperatura_Real (Temperatura medida pelo sensor, °C) - Saida_Controlador (Sinal de controle enviado ao aquecedor, %)

Código Python:

import numpy as np
import matplotlib.pyplot as plt
# 1. Simulação de dados
np.random.seed(42)  # Para reprodutibilidade
tempo = np.arange(0, 100, 1)  # Tempo de 0 a 99 segundos
setpoint = np.where(tempo < 50, 50, 70)  # Setpoint muda de 50°C para 70°C em t=50s
temperatura_real = 50 + 0.5 * (tempo - 50) + np.random.normal(0, 1, len(tempo))  # Resposta do sistema com ruído
saida_controlador = np.clip(0.5 * (setpoint - temperatura_real), 0, 100)  # Saída do controlador proporcional
# 2. Criação do gráfico
plt.figure(figsize=(12, 6))
plt.plot(tempo, setpoint, label='Setpoint (Temperatura Desejada)', color='blue', linestyle='--')
plt.plot(tempo, temperatura_real, label='Temperatura Real', color='red')
plt.plot(tempo, saida_controlador, label='Saída do Controlador', color='green')
plt.title('Análise do Desempenho de um Sistema de Controle de Temperatura')
plt.xlabel('Tempo (s)')
plt.ylabel('Temperatura (°C) / Saída do Controlador (%)')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()

Saída Esperada:

Gráfico mostrando as curvas de setpoint, temperatura real e saída do controlador ao longo do tempo.

Resultados do Gráfico

Gráfico mostrando as curvas de setpoint, temperatura real e saída do controlador ao longo do tempo.

Análise do Gráfico

O gráfico gerado apresenta três curvas principais: - Setpoint (Temperatura Desejada): Representada pela linha azul tracejada, mostra a temperatura alvo que o sistema deve atingir. Neste exemplo, o setpoint muda de 50°C para 70°C no tempo t=50 segundos. - Temperatura Real: Representada pela linha vermelha, mostra a temperatura medida pelo sensor ao longo do tempo. A resposta do sistema apresenta um comportamento típico de controle, com uma tendência a seguir o setpoint, mas com algum atraso e flutuação devido a ruídos. - Saída do Controlador: Representada pela linha verde, indica o sinal de controle enviado ao aquecedor. Este sinal é proporcional à diferença entre o setpoint e a temperatura real, ajustando-se para minimizar o erro.

Interpretação do Desempenho do Sistema

A partir do gráfico, podemos analisar o desempenho do sistema de controle: - Tempo de Subida: O tempo que leva para a temperatura real atingir o novo setpoint após a mudança. Neste caso, é visível que a temperatura leva algum tempo para se ajustar ao novo setpoint de 70°C. - Overshoot: A temperatura real ultrapassa temporariamente o setpoint antes de estabilizar. Isso pode ser observado logo após a mudança do setpoint, onde a temperatura real sobe acima de 70°C antes de se estabilizar. - Tempo de Assentamento: O tempo que leva para a temperatura real se estabilizar dentro de uma faixa aceitável em torno do setpoint. Neste exemplo, a temperatura parece se estabilizar em torno de 70°C após alguns segundos. - Erro em Regime Permanente: A diferença entre o setpoint e a temperatura real após o sistema se estabilizar. Idealmente, esse erro deve ser minimizado, e neste exemplo, a temperatura real parece se aproximar do setpoint de 70°C.

Resumindo, a visualização dessas curvas permite identificar rapidamente o desempenho do sistema de controle, facilitando ajustes e otimizações necessárias para melhorar a resposta do sistema.

7.4. Conclusão

A visualização de dados é uma habilidade essencial para engenheiros e cientistas, permitindo a interpretação clara e eficaz de informações complexas. Neste módulo, exploramos os principais tipos de gráficos utilizados na visualização de dados, como gráficos de linha, barras, dispersão e histogramas, e discutimos suas aplicações práticas em engenharia. Através de exemplos práticos, aprendemos a utilizar as bibliotecas MAT_PLOT_LIB e SEABORN para criar gráficos informativos e visualmente atraentes. A capacidade de visualizar dados de forma eficaz é crucial para a análise de desempenho de sistemas, identificação de tendências e comunicação de resultados.

8. Cálculo Numérico com NUM_PY

No universo da engenharia, a capacidade de realizar cálculos numéricos eficientes e complexos é de suma importância. Este módulo nos levará ao coração do Cálculo Numérico com NUM_PY, uma biblioteca fundamental em Python que revoluciona a forma como lidamos com dados matemáticos. Começaremos explorando os arrays e operações vetoriais, que são a base do NUM_PY, entendendo como eles permitem realizar operações matemáticas de forma rápida e otimizada em grandes conjuntos de dados. Em seguida, aprofundaremos no conceito de matrizes e álgebra linear, mostrando como o NUM_PY simplifica operações complexas como multiplicação de matrizes, inversão e resolução de sistemas. Por fim, veremos as aplicações práticas em balanços e sistemas lineares, demonstrando como essas ferramentas podem ser utilizadas para resolver problemas reais de engenharia, desde balanços de massa e energia até a análise de circuitos e estruturas. Ao final deste módulo, você estará apto a utilizar o NUM_PY para realizar cálculos numéricos robustos e eficientes, essenciais para diversas disciplinas da engenharia.

8.1. Arrays e Operações Vetoriais

No coração do NUM_PY (Numerical Python) está o objeto ndarray (N-dimensional array), uma estrutura de dados fundamental para computação numérica eficiente. Diferente das listas Python, que podem armazenar elementos de tipos variados, os arrays NUM_PY são homogêneos, ou seja, todos os seus elementos devem ser do mesmo tipo de dado (inteiro, FLOAT etc.). Essa característica, combinada com a implementação em C, torna as operações com arrays NUM_PY incrivelmente mais rápidas e eficientes em termos de memória para grandes volumes de dados numéricos.

8.1.1. O que são Arrays NUM_PY?

Um array NUM_PY é uma grade de valores, todos do mesmo tipo, e é indexado por uma tupla de inteiros não negativos. O número de dimensões é o rank do array. - Vetor: Um array 1-D (uma dimensão). - Matriz: Um array 2-D (duas dimensões). - Tensor: Um array com 3 ou mais dimensões.

Vantagens sobre Listas Python: - Velocidade: Operações matemáticas em arrays NUM_PY são executadas muito mais rapidamente. - Memória: Arrays NUM_PY consomem menos memória para armazenar grandes quantidades de dados do mesmo tipo. - Funcionalidade: Oferecem uma vasta gama de funções matemáticas e de álgebra linear otimizadas.

8.1.2. Criação de Arrays

Os Arrays podem ser criados de diversas formas: - A partir de listas Python: Usando np.array(). - Arrays preenchidos com valores específicos: np.zeros(), np.ones(), np.full(). - Arrays com sequências numéricas: np.arange(), np.linspace(). - Arrays com valores aleatórios: np.random.rand(), np.random.randn().

Atributos Importantes de um Array: - ndim: O número de dimensões do array. - shape: Uma tupla indicando o tamanho de cada dimensão. - size: O número total de elementos no array. - dtype: O tipo de dado dos elementos no array.